Gọi x;y lần lượt là thời gian làm riêng để người thứ nhất và người thứ hai hoàn thành công việc (ngày) (x>4; y>6)
Một ngày người thứ nhất làm được: \(\dfrac{1}{x}\) (CV)
Một ngày người thứ hai làm được: \(\dfrac{1}{y}\) (CV)
Vì hai người làm chung thì hoàn thành công việc trong 4 ngày, một ngày hai người làm được: \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{4}\) (CV) (1)
Hai ngày hai người làm chung được: \(2.\dfrac{1}{4}=\dfrac{1}{2}\) (CV)
Trong 6 ngày thì người thứ hai làm một mình được: \(\dfrac{6}{y}\) (CV)
Ta có pt: \(\dfrac{1}{2}+\dfrac{6}{y}=1\) \(\Leftrightarrow y=12\) (Thỏa mãn)
Thay y=12 vào (1) \(\Rightarrow\dfrac{1}{x}+\dfrac{1}{12}=\dfrac{1}{4}\Leftrightarrow x=6\) (Thỏa mãn)
Vậy người thứ nhất làm một mình trong 6 ngày thì hoàn thành CV, người thứ hai làm một mình trong 12 ngày thì hoàn thành CV







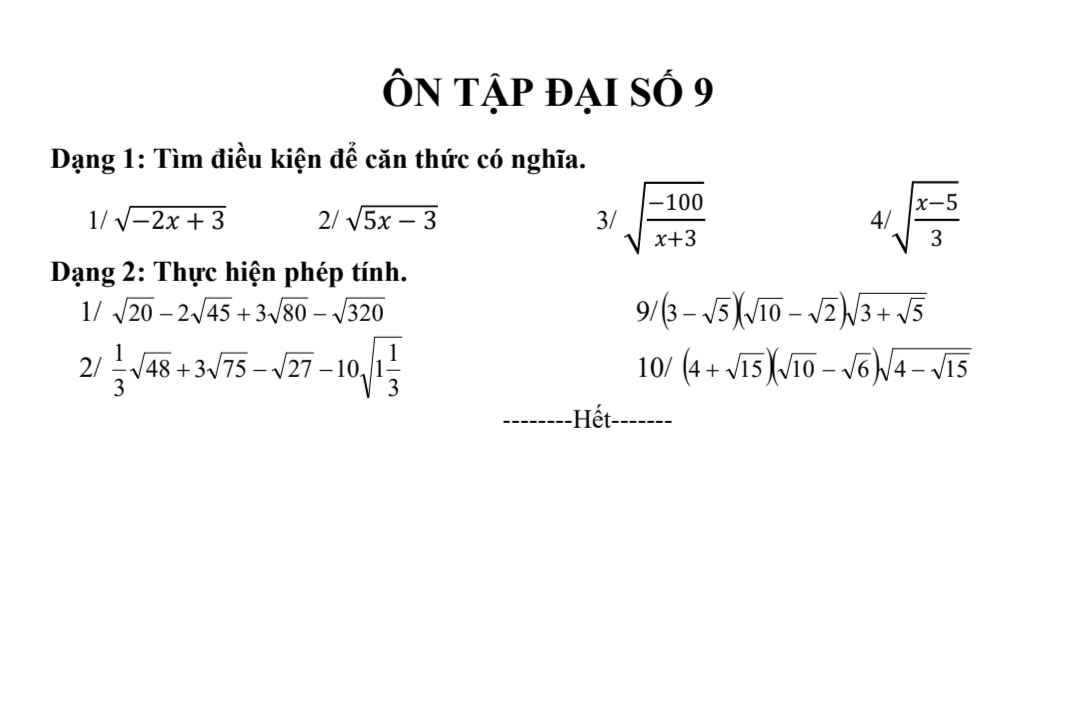

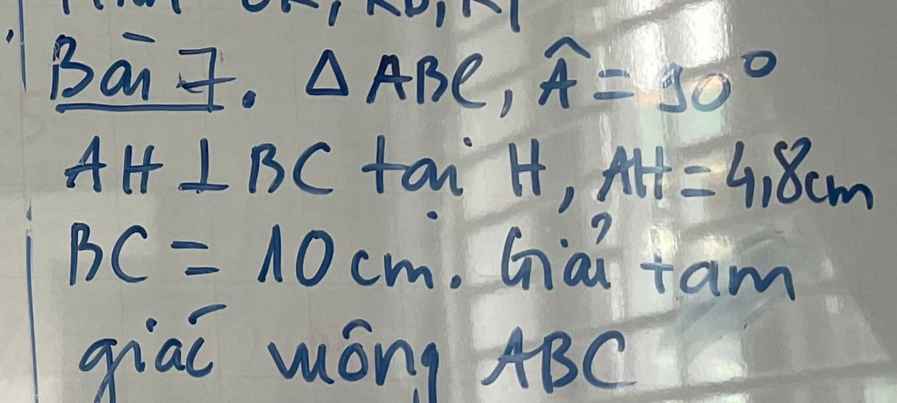


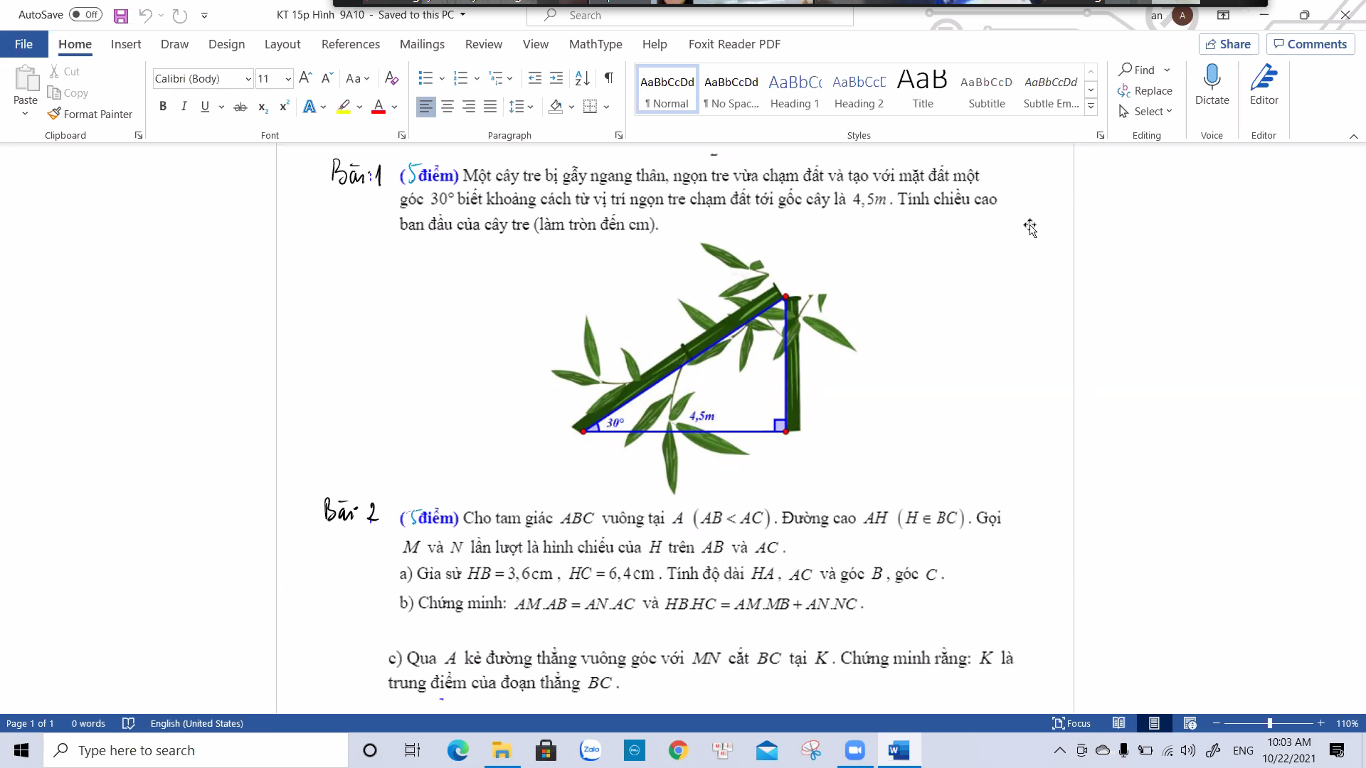





 Ai giúp em với ạ em cần rất gấp bài 4 thôi ạ
Ai giúp em với ạ em cần rất gấp bài 4 thôi ạ
 em cần giải gấp bài 2 ạ, mọi người giúp em với ạ
em cần giải gấp bài 2 ạ, mọi người giúp em với ạ

 giúp em với ạ, cần gấp ạ TvT
giúp em với ạ, cần gấp ạ TvT