Các câu hỏi tương tự
Trong mặt phẳng với hệ trục tọa đô Oxy , cho hai đường thẳng ∆1: x- y+ 1 0 và ∆2: 2x + y-1 0 và điểm P (2;1) .Viết phương trình đường thẳng đi qua điểm P và cắt hai đường thẳng ∆1, ∆2 lần lượt tại hai điểm A: B sao cho P là trung điểm AB? A. 4x – y- 7 0 B. x+ 4y- 4 0 C. x- 4y-7 0 D . 2x + y- 7 0
Đọc tiếp
Trong mặt phẳng với hệ trục tọa đô Oxy , cho hai đường thẳng ∆1: x- y+ 1= 0 và ∆2: 2x + y-1 = 0 và điểm P (2;1) .Viết phương trình đường thẳng đi qua điểm P và cắt hai đường thẳng ∆1, ∆2 lần lượt tại hai điểm A: B sao cho P là trung điểm AB?
A. 4x – y- 7 = 0
B. x+ 4y- 4= 0
C. x- 4y-7= 0
D . 2x + y- 7= 0
Trong mặt phẳng với hệ trục tọa đô, cho hai đường thẳng x+ y-1 0 và 3x –y+ 5 0. Hãy tìm diện tích hình bình hành có hai cạnh nằm trên hai đường thẳng đã cho, một đỉnh là giao điểm của hai đường thẳng đó và giao điểm của hai đường chéo là I(3;3). A. 74 B. 55 C. 54 D. 65.
Đọc tiếp
Trong mặt phẳng với hệ trục tọa đô, cho hai đường thẳng x+ y-1= 0 và 3x –y+ 5= 0. Hãy tìm diện tích hình bình hành có hai cạnh nằm trên hai đường thẳng đã cho, một đỉnh là giao điểm của hai đường thẳng đó và giao điểm của hai đường chéo là I(3;3).
A. 74
B. 55
C. 54
D. 65.
trong mặt phẳng oxy, cho đường tròn (C):\(x^2+y^2-8x+6y+ 21=0\) và đường thẳng d: \(x+ y-1=0\)
Hai tiếp tuyến của đường tròn C tại A,B vuông góc với nhau tại điểm N. Biết N thuộc đường thẳng d. Tìm toạ độ điểm N
cho tam giác ABC có A(-2;3) vá hai đường trung tuyến qua điểm B và điểm C lần lượt là 2x-y+1= 0 , x+y-4=0. Hãy viết phương trình ba đường thẳng chứa ba cạnh của tam giác.
Trong mặt phẳng với hệ trục tọa độ Oxy; tam giác ABC có đỉnh A( 2;-3) ; B( 3;-2) và diện tích tam giác ABC bằng 3/2. Biết trọng tâm G của tam giác ABC thuộc đường thẳng d: 3x- y- 8 0. Tìm tọa độ điểm C. A. C( -1; 1) và C( 2 ; -3) B. C( 1;-1)và C( -2 ; 10) C. ( 1;-1) và C(2 ; -6) D. C( 1;1) và C( 2 ; -3)
Đọc tiếp
Trong mặt phẳng với hệ trục tọa độ Oxy; tam giác ABC có đỉnh A( 2;-3) ; B( 3;-2) và diện tích tam giác ABC bằng 3/2. Biết trọng tâm G của tam giác ABC thuộc đường thẳng d: 3x- y- 8= 0. Tìm tọa độ điểm C.
A. C( -1; 1) và C( 2 ; -3)
B. C( 1;-1)và C( -2 ; 10)
C. ( 1;-1) và C(2 ; -6)
D. C( 1;1) và C( 2 ; -3)
(C) tâm I (-3;1) và tiếp xúc với đường thẳng d 3x-4y+1=0
Đường thẳng đi qua hai điểm A(1;-2) và B(-2;0) có hệ số góc là
A. 2 3
B. - 2 3
C. 2
D. 1 2
Cho elíp
E
:
x
2
25
+
y
2
9
1
và đường thẳng d: x- 2y +12 0. điểm M trên (E) sao cho khoảng cách từ điểm M đến đường thẳng d là lớn nhất, nhỏ nhất.Tìm GTLN; GTNN đó? D. Đáp án khác
Đọc tiếp
Cho elíp E : x 2 25 + y 2 9 = 1 và đường thẳng d: x- 2y +12= 0. điểm M trên (E) sao cho khoảng cách từ điểm M đến đường thẳng d là lớn nhất, nhỏ nhất.Tìm GTLN; GTNN đó?
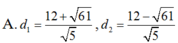
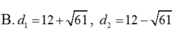
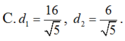
D. Đáp án khác
Cho parabol
P
x
2
+
3
x
-
2
và đường thẳng
∆
x
-
m
.Tập hợp tất cả các giá trị của m để
∆
cắt (P) tại hai điểm phân biệt là A.
-
∞
;
1
B.
1
;...
Đọc tiếp
Cho parabol P = x 2 + 3 x - 2 và đường thẳng ∆ = x - m .
Tập hợp tất cả các giá trị của m để ∆ cắt (P) tại hai điểm phân biệt là
A. - ∞ ; 1
B. 1 ; + ∞
C. - 2 ; + ∞
D. - 2 ; 1







