Question

Dựng góc 75 0  bằng thước và compa.

Answer 1

Cách dựng:

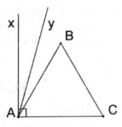
- Dựng ∆ ABC đều

- Trên nửa mặt phẳng bờ AC chứa điểm B dựng tia Ax ⊥ AC

- Dựng tia phân giác Ay của ∠ (xAB)

Ta có: ∠ (CAy) =  75 0

Chứng minh: Thật vậy,  ∆ ABC đều nên  ∠ (BAC) =  60 0 , ∠ (xAC) =  90 0

⇒  ∠ (BAx) =  ∠ (xAC) -  ∠ (BAC)

⇒  ∠ (BAx) =  90 0  –  60 0  =  30 0

⇒  ∠ (BAy) = 1/2  ∠ (BAx) = 1/2. 30 0 =  15 0

Do đó,  ∠ (CAy) =  ∠ (CAB) +  ∠ (BAy) =  60 0  +  15 0  =  75 0