Chọn A
Ta có: y ' = 2 - 2 x 3 1 + 4 x - x 4 . y ' = 0
![]()
Chọn A
Ta có: y ' = 2 - 2 x 3 1 + 4 x - x 4 . y ' = 0
![]()
Tìm tất cả các giá trị thực của tham số m để hàm số y = x 3 - 3 m x 2 + 3 ( m 2 - 1 ) x - m 3 + m có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số đến gốc tọa độ O bằng 2 lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến gốc tọa độ O
A. m = - 3 - 2 2 h o ặ c m = - 1
B. m = - 3 + 2 2 h o ặ c m = - 1
C. m = - 3 + 2 2 h o ặ c m = - 3 - 2 2 .
D. m = - 3 + 2 2
Với giá trị nào của m, đồ thị hàm số y = x 3 – m x 2 + 3 ( m 2 - 1 ) x – m 3 + m có điểm cực đại B, điểm cực tiểu C thỏa mãn OC = 3OB, với O là gốc tọa độ?
A. m = 2 hoặc m = 1 2
B. m = 2
C. m = 1 2
D. m = - 1 2 hoặc m = 1 2
Tính tổng tất cả các giá trị thực của tham số m để hàm số y= x3-3mx2+ 3( m2-1) x- m3+ m có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số đến gốc tọa độ O bằng 2 lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến gốc tọa độ O.
A. -4
B. -5
C. -6.
D. -7
Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình dưới đây.
(I). Hàm số nghịch biến trên khoảng (0;1).
(II). Hàm số đồng biến trên khoảng (-1;2).
(III). Hàm số có ba điểm cực trị.
(IV). Hàm số có giá trị lớn nhất bằng 2.
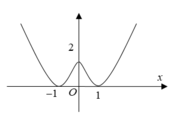
Số mệnh đề đúng trong các mệnh đề sau là:
A. 4
B. 2
C. 3
D. 1
Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình dưới đây.
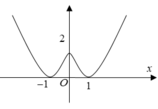
(I). Hàm số nghịch biến trên khoảng (0;1).
(II). Hàm số đồng biến trên khoảng (-1;2).
(III). Hàm số có ba điểm cực trị.
(IV). Hàm số có giá trị lớn nhất bằng 2
Số mệnh đề đúng trong các mệnh đề sau là:
A. 4
B. 2
C. 3
D. 1
Cho hàm số y = a x 3 + b x 2 + c x + d . Nếu đồ thị hàm số có 2 điểm cực trị là gốc tọa độ và điểm A ( - 1 ; - 1 ) thì hàm số có phương trình là
A. y = 2 x 3 - 3 x 2 .
B. y = - 2 x 3 - 3 x 2 .
C. y = x 3 + 3 x 2 + 3 x .
D. y = x 3 - 3 x - 1 .
Cho hàm số y = a x 3 + b x 2 + c x + d . Nếu đồ thị hàm số có 2 điểm cực trị là gốc tọa độ và điểm A(-1; -1) thì hàm số có phương trình là:
A. y ' = 2 x 3 - 3 x 2
B. y ' = - 2 x 3 - 3 x 2
C. y ' = x 3 + 3 x 2 + 3 x
D. y ' = x 3 - 3 x - 1
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d ( v ớ i a , b , c , d ∈ ℝ , a > 0 ) . Biết đồ thị hàm số y=f(x) này có điểm cực đại A (0;1) và điểm cực tiểu B(2;-3). Hỏi tập nghiệm của phương trình f 3 ( x ) + f ( x ) - 2 f ( x ) 3 = 0 có bao nhiêu phần tử?
A. 2019
B. 2018
C. 9
D. 8
Có bao nhiêu giá trị nguyên của tham số m để hàm số y = - x 3 + 3 x 2 + 3 ( m 2 - 1 ) x - 3 m 2 - 1 có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số cách đều gốc tọa độ O.
A. 0
B. 1
C. 2
D. 3
Cho hàm số y= x4-2( m+1)x2+ m ( C). Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số C có ba điểm cực trị A: B; C sao cho OA= BC ; trong đó O là gốc tọa độ, A là điểm cực trị thuộc trục tung, B và C là hai điểm cực trị còn lại.
A. m = 2 ± 2 2
B. m = 2 + 2 2
C. m = 2 - 2 2
D. m = ± 1