`(x+1)/2009+(x+3)/2007=(x+5)/2005+(x+7)/1993`
`<=>(x+1)/2009+1+(x+3)/2007+1=(x+5)/2005+1+(x+7)/1993+1`
`<=>(x+2020)/2009+(x+2020)/2007=(x+2020)/2005+(x+2020)/1993`
`<=>(x+2020)(1/2009+1/2007-1/2005-1/1993)=0`
`<=>x+2020=0`
`<=>x=-2020`
Vậy `S={-2020}`
Đúng 0
Bình luận (1)








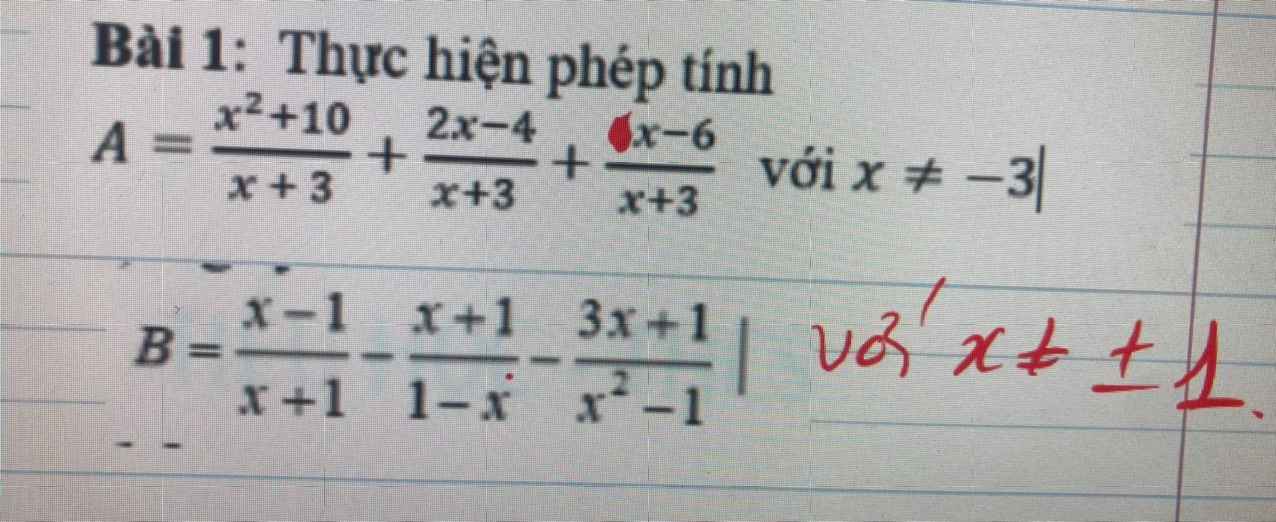






 Cứu
Cứu 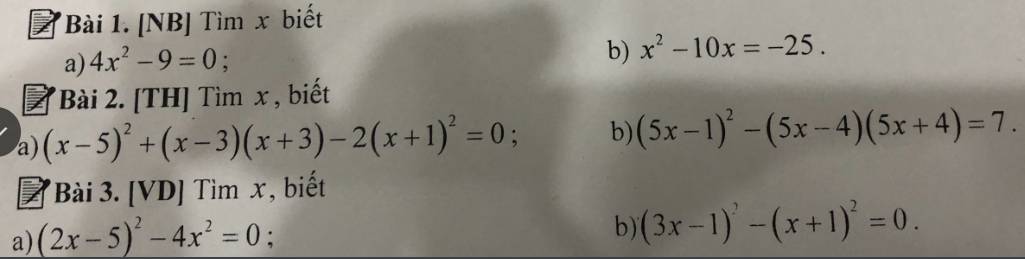



 cứu với
cứu với