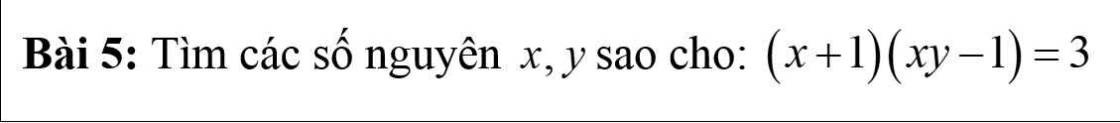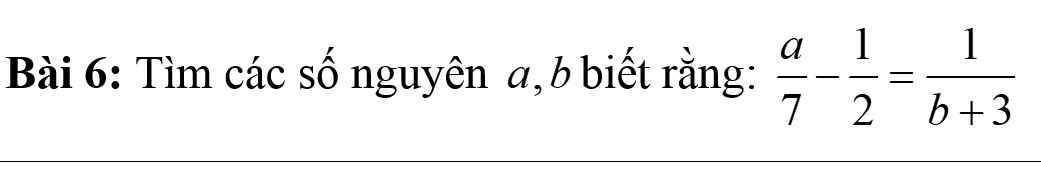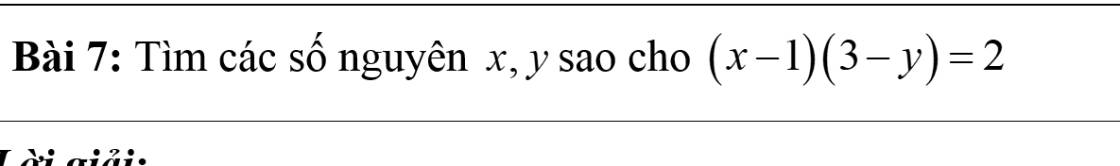Question

   cứu mik mấy ní oi 

Answer 1

Bài 5:

Với $x,y$ là số nguyên thì $x+1, xy-1$ cũng là số nguyên. Mà tích của chúng bằng 3 nên ta có các TH sau:

TH1: $x+1=1, xy-1=3\Rightarrow x=0; xy=3$ (vô lý - loại) 

TH2: $x+1=-1, xy-1=-3\Rightarrow x=-2; xy=-2\Rightarrow y=1$ (thỏa mãn) 

TH3: $x+1=3; xy-1=1\Rightarrow x=2; xy=2\Rightarrow y=1$ (thỏa mãn)

TH4: $x+1=-3; xy-1=-1\Rightarrow x=-4; xy=0$ (vô lý -loại)

Vậy......

Answer 2

Bài 6:

$\frac{a}{7}-\frac{1}{2}=\frac{1}{b+3}$

$\Rightarrow \frac{2a-7}{14}=\frac{1}{b+3}$

$\Rightarrow (2a-7)(b+3)=14$

Với $a,b$ nguyên thì $2a-7, b+3$ cũng là số nguyên. Mà $(2a-7)(b+3)=14$ và $2a-7$ là số nguyên lẻ nên ta các TH sau:

TH1: $2a-7=1; b+3=14\Rightarrow a=4; b=11$ (thỏa mãn) 

TH2: $2a-7=-1; b+3=-14\Rightarrow a=3; b=-17$ (thỏa mãn) 

TH3: $2a-7=7; b+3=2\Rightarrow a=7; b=-1$ (thỏa mãn) 

TH4: $2a-7=-7; b+3=-2\Rightarrow a=0; b=-5$ (thỏa mãn)

Answer 3

Bài 7:

Với $x,y$ nguyên thì $x-1, 3-y$ cũng nguyên. Mà $(x-1)(3-y)=2$ nên ta có các TH sau:
TH1: $x-1=1, 3-y=2\Rightarrow x=2; y=1$ (thỏa mãn)

TH2: $x-1=-1; 3-y=-2\Rightarrow x=0; y=5$ (thỏa mãn) 

TH3: $x-1=3; 3-y=1\Rightarrow x=4; y=2$ (thỏa mãn) 

TH4: $x-1=-3; 3-y=-1\Rightarrow x=-2; y=4$ (thỏa mãn)