Có N 1 bóng đèn cùng loại 3 V - 3 W và N 2 nguồn điện có cùng suất điện động E 0 = 4 V và điện trở trong r 0 = 1 Ω được mắc thành bộ nguồn hỗn hợp đối xứng. Nếu số nguồn là N 2 = 15 thì có thể thắp sáng bình thường số đèn lớn nhất ( N 1 max) là bao nhiêu ? Vẽ sơ đồ tất cả các cách mắc nguồn và đèn khi đó và tính hiệu suất của bộ nguồn đối với từng cách mắc đó.
Nếu số nguồn là N 2 = mn = 15 và với số đèn là N 1 = xy ta cũng có phương trình (1) và bất đẳng thức (2) trên đây. Kết quả là trong trường hợp này ta có :
3yn + xm = 4mn ≥ 2. 3 m n x y hay 60 ≥ 2. 45 N 1
Từ đó suy ra : N 1 ≤ 20. Vậy với~số nguồn là N 2 = 15 thì có thể thắp sáng bình thường số đèn lớn nhất là N 1 = 20.
Để tìm được cách mắc nguồn và đèn trong trường hợp này ta có xỵ = 20 hay y = 20/x. Thay giá trị này vào phương trình (1) ta đi tới phương trình :
m x 2 – 60x + 60n = 0
Phương trình này có nghiêm kép ( ∆ ' = 0) là : x = 30/m.
Chú ý rằng x, y, n và m đều là số nguyên, dương nên ta có bảng các trị số này như sau :
| m | n | x | y |
| 3 | 5 | 10 | 2 |
| 15 | 1 | 2 | 10 |
Như vậy trong trường hợp này chỉ có hai cách mắc các nguồn và các bóng đèn là :
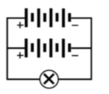
- Cách một : Bộ nguồn gồm n = 5 dãy song song, mỗi dãy gồm m - 3 nguồn mắc nối tiếp và các bóng đèn được mắc thành X - 10 dãy song song với mỗi dãy gồm y - 2 bóng đèn mắc nối tiếp (Hình 11.6Ga).
Cách mắc này có hiệu suất là : H 1 = 6/12 = 50%
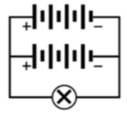
- Cách hai : Bộ nguồn gồm n = 1 dãy có m = 15 nguồn mắc nối tiếp và các bóng đèn được mắc thành x = 2 dãy song song với mỗi dãy gồm y = 10 bóng đèn mắc nối tiếp (Hình 11.6Gb).
Cách mắc này có hiệu suất là : H 2 = 30/60 = 50%