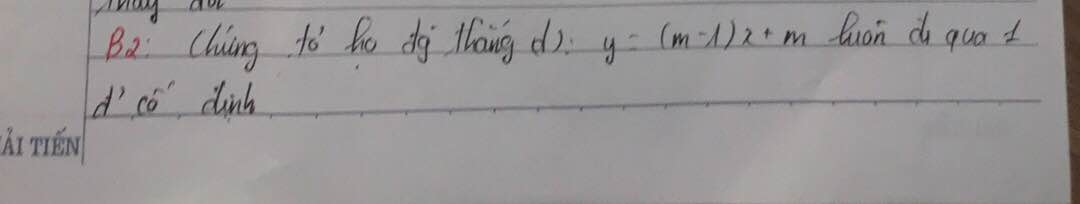Question

Chứng tỏ đường thẳng (d): y=(m-1)x+m luôn đu qua 1 điểm cố định

Answer 1

Giả sử đường thẳng luôn đi qua điểm cố định \(M\left(x_0;y_0\right)\), khi đó với mọi m ta luôn có:

\(y_0=\left(m-1\right)x_0+m\)

\(\Leftrightarrow m\left(x_0+1\right)-x_0-y_0=0\)

\(\Leftrightarrow\left\{{}\begin{matrix}x_0+1=0\\-x_0-y_0=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x_0=-1\\y_0=1\end{matrix}\right.\)

Vậy với mọi m thì họ đường thẳng d luôn đi qua điểm cố định \(M\left(-1;1\right)\)