Kí hiệu như hình vẽ
Tam giác ABC cân nên góc EBC = góc DCB (1)
Ta có + Góc ECB=180-CEB-EBC=90-EBC (2)
+Góc DBC=180-BDC-DCB=90-DCB (3)
Từ (1),(2),(3)=>Góc ECB=Góc DCB
Xét tam giác EBC và tam giác DCB có
+Góc EBC = Góc DCB (Chứng minh trên)
+BC-Cạnh chung
+Góc ECB=Góc DCB (Chứng minh trên)
=>Tam giác EBC=Tam giác DCB (g.c.g)
=>EC=DB (2 cạnh tương ứng )
=>Điều phải chứng minh
Trả lời:
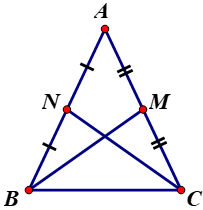
Giả sử ΔABC cân tại A có hai đường trung tuyến BM và CN, ta cần chứng minh BM = CN.
Ta có: AC = 2.AM, AB = 2. AN, AB = AC (vì ΔABC cân tại A)
⇒ AM = AN.
Xét ΔABM và ΔACN có:
AM = AN
AB = AC
Góc A chung
⇒ ΔABM = ΔACN (c.g.c) ⇒ BM = CN (hai cạnh tương ứng).
(Còn một số cách chứng minh khác, nhưng do giới hạn kiến thức lớp 7 nên mình xin sẽ không trình bày.)