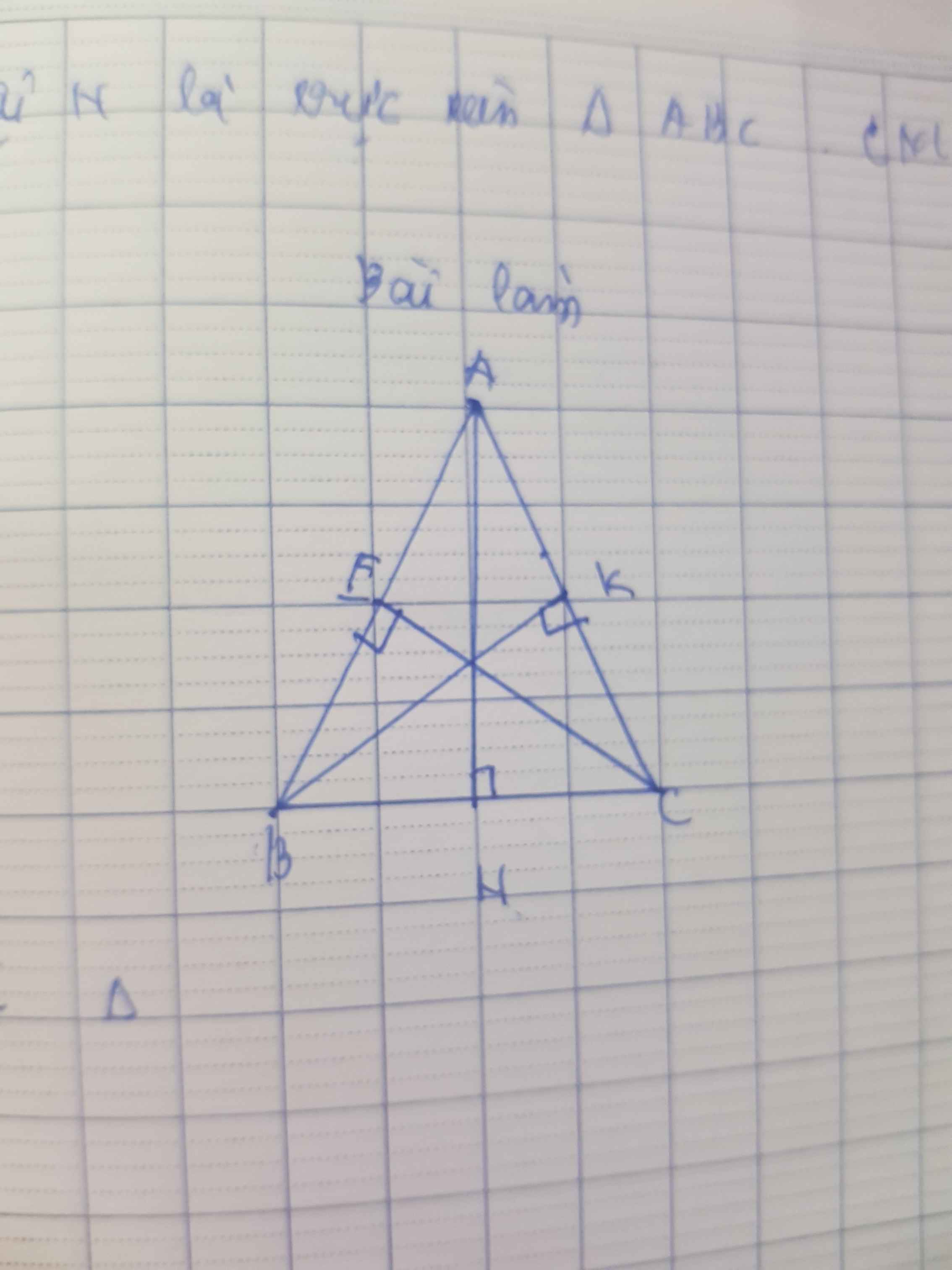
xét tam giác BFC và tg CKB
\(gBFC=gCKB\left(gt\right)\\
CF=BK\left(gt\right)\\
BC:CHUNG\)
=> 2 tg bằng nhau (c-g-c)
=> góc FBC = góc KCB(2 góc t/ư)
chứng minh tương tự với tg FBC và tg KAB (c-g-c)
=> gBAC = gABC (2 góc t/ư )
=> gBAC = gABC = gACB = \(\dfrac{180}{3}\) = 60o
=> tg ABC đều
Đúng 4
Bình luận (0)
Các câu hỏi tương tự
Chứng minh 1 tam giác có 3 đường cao bằng nhau thì đó là tam giác đều
Giúp mình vs
Chứng minh rằng 1 tam giác có 2 đường cao (xuất phát từ các đỉnh của 2 góc nhọn) bằng nhau thì tam giác đó là tam giác cân. Từ đó suy ra 1 tam giác có 3 đường cao bằng nhau là tam giác đều
Chứng minh phần " tam giác có 3 đường cao bằng nhau " giúp mình nha. Phần " tam giác có 2 đường cao bằng nhau " mình tự làm được
bài 1: chứng minh 1 tam có 2 đường trung tuyến bằng nhau thì tam giác đó cân
bài 2: chứng minh trong tam giác cân 2 đường cao ứng với 2 cạnh bên và ngược lại có 2 đường cao bằng nhau là tam giác cân
bài 3:chứng minh 2 đường phân giác xuất phát từ 2 đỉnh ở đấy của tam giác cân thì bằng nhau và ngược lại 1 tam giác có 2 đg phân giác bằng nhau thì là tam giác ân
Chứng minh một tam giác có 2 đường cao (xuất phát từ các đỉnh của 2 góc nhọn) bằng nhau thì tam giác đó là tam giác cân.Từ đó suy ra một tam giác có 3 đường cao bằng nhau thì tam giác đó là tam giác đều.
Chứng minh rằng tam giác có 3 đường cao bằng nhau thì tam giác đó là tam giác đều.
Chứng minh rằng một tam giác có hai đường đường cao(xuất phát từ các đỉng của hai góc nhọn) bằng nhau thì tam giác đó là tam giác cân. Từ đó suy ra một tam giác có ba đường cao bằng nhau thì tam giác đó là tam giác đều.
Chứng minh rằng một tam giác có hai đường cao (xuất phát từ các đỉnh của hai góc nhọn) bằng nhau thì tam giác đó là tam giác cân. Từ đó suy ra một tam giác có ba đường cao bằng nhau thì tam giác đó là tam giác đều.
mạng mạng
Chứng minh rằng tam giác có ba đường cao bằng nhau là tam giác đều
Cho tam giác ABC có đường cao AH và trung tuyến AM chia góc A ra thành 3 góc bằng nhau. Chứng minh tam giác ABC là tam giác vuông và tam giác ABM là tam giác đều.