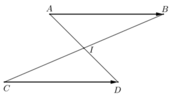
Gọi trung điểm của AD là I, trung điểm BC là J.
Khi đó ta có: 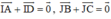
Mà theo quy tắc ba điểm ta có:
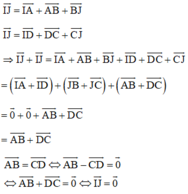
⇔ I ≡ J hay trung điểm AD và BC trùng nhau (đpcm)

Gọi trung điểm của AD là I, trung điểm BC là J.
Khi đó ta có: 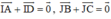
Mà theo quy tắc ba điểm ta có:
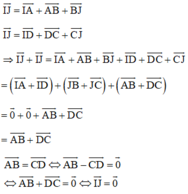
⇔ I ≡ J hay trung điểm AD và BC trùng nhau (đpcm)
Cho tam giác ABC nhọn với AB<BC và D là điểm thuộc cạnh BC sao cho AD là phân giác của B A C ^ .
Đường thẳng qua C và song song với AD, cắt trung trực của AC tại E.
Đường thẳng qua B song song với AD, cắt trung trực của AB tại F.
1) Chứng minh rằng tam giác ABF đồng dạng với tam giác ACE.
2). Chứng minh rằng các đường thẳng B E ; C F ; A D đồng quy tại một điểm, gọi điểm đó là G.
3). Đường thẳng qua G song song với AE cắt đường thẳng BF tại Q. Đường thẳng QE, cắt đường tròn ngoại tiếp tam giác GEC tại P khác E. Chứng minh rằng các điểm A, P, G, Q, F cùng thuộc một đường tròn.
Các điểm A'(-4; 1), B'(2; 4), C'(2; -2) lần lượt là trung điểm các cạnh BC, CA và AB của tam giác ABC. Tính tọa độ các đỉnh của tam giác ABC. Chứng minh rằng trọng tâm của tam giác ABC và A'B'C' trùng nhau.
Cho tam giác ABC nhọn nội tiếp đường tròn (O). H là trực tâm của tam giác ABC.
AD là đường kính của (O). E thuộc AC sao cho HE//BC.
1). Chứng minh rằng các đường thẳng BH và DE cắt nhau trên (O)
2). Gọi F là giao điểm của các đường thẳng EH và AB. Chứng minh rằng A là tâm đường tròn bàng tiếp ứng với đỉnh D của tam giác DEF
3). Gọi I là tâm đường tròn nội tiếp của tam giác DEF. Chứng minh rằng BE, CF và IH đồng quy.
Cho 4 điểm A,B,C,D phân biệt .CMR \(\overrightarrow{AB}=\overrightarrow{CD}\) \(\Leftrightarrow\)Trung điểm các đoạn AD và BC trùng nhau
Cho tam giác ABC, trên cạnh BC lấy điểm D sao cho BD= 2/3 BC, M là trung điểm của đoạn thẳng AD, điểm N thoả mãn điều kiện vectơ AN = 2/5 vectơ AC. Chứng minh 3 điểm B , M ,N thẳng hàng.
Cho tam giác ABC vuông tại A, góc B = 60. Gọi I là trung điểm cạnh BC.Trên các cạnh AB,AC lần lượt lấy các điểm M,N.Chứng minh rằng MI vuông góc với NI khi và chỉ khi BM + căn 3 CN = BC
Cho tứ giác ABCD nội tiếp đường tròn Γ có tâm O. Các điểm P và Q theo thứ tự nằm
trên các cạnh BC, DA. Biết rằng trung điểm của các đoạn thẳng AP, BQ, CQ và DP cùng
nằm trên đường tròn k. Chứng minh rằng OP = OQ.
1 bài hình khó .
Cho tam giác ABC và điểm M nằm trong tam giác. Gọi AM, BM, CM cắt BC, CA, AB lần lượt tại A', B', C'. Chứng minh rằng M là trọng tâm tam giác ABC khi và chỉ khi M là trọng tâm tam giác A'B'C'
Cho tam giác ABC, gọi D là điểm trên cạnh BC sao cho vecto BD=2/3 vecto BC và I là trung điểm của AD. Gọi M là điểm thỏa mãn vecto AM=2/5 vecto AC. Chứng minh B,I,M thẳng hàng