Question

Chứng minh rằng: "Hai tia phân giác của hai góc đối đỉnh là hai tia đối nhau.

Answer 1

?¿‽

Answer 2

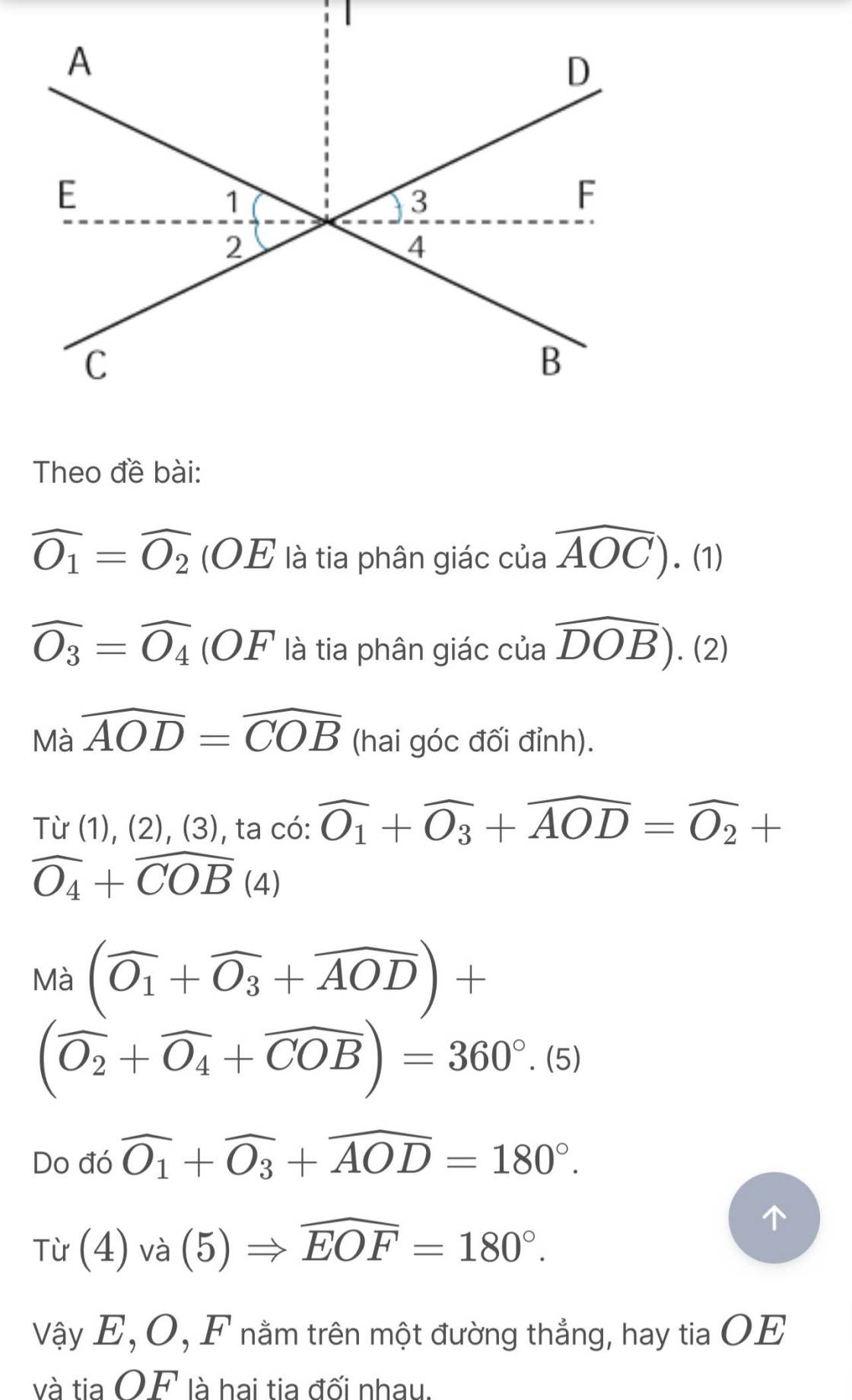
Ta có A O C ^ = B O D ^  (hai góc đối đỉnh) mà O 1 ^ = O 2 ^ ; O 3 ^ = O 4 ^  nên O 1 ^ = O 3 ^  (một nửa của hai góc bằng nhau).

⇒ A O D ^ + O 4 ^ + O 3 ^ = 180 °

Do đó M O N ^ = 180 ° .

Suy ra hai tia OM, ON đối nhau

Answer 3

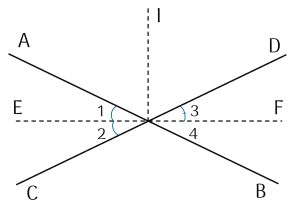
Theo đề bài:

\widehat{{O}_{1}}=\widehat{{O}_{2}}O1​​=O2​​ ($OE$ là tia phân giác của \widehat{AOC}) .AOC). (1)

\widehat{{O}_{3}}=\widehat{{O}_{4}}O3​​=O4​​ ($OF$ là tia phân giác của \widehat{DOB})DOB). (2)

Mà \widehat{{AOD}}=\widehat{{COB}}AOD=COB (hai góc đối đỉnh).

Từ (1), (2), (3), ta có: \widehat{{O}_{1}}+\widehat{{O}_{3}}+\widehat{{AOD}}=\widehat{{O}_{2}}+\widehat{{O}_{4}}+\widehat{{COB}}O1​​+O3​​+AOD=O2​​+O4​​+COB (4)

Mà \left(\widehat{{O}_{1}}+\widehat{{O}_{3}}+\widehat{{AOD}}\right)+\left(\widehat{{O}_{2}}+\widehat{{O}_{4}}+\widehat{{COB}}\right)=360^{\circ}(O1​​+O3​​+AOD)+(O2​​+O4​​+COB)=360∘. (5)

Do đó \widehat{{O}_{1}}+\widehat{{O}_{3}}+\widehat{{AOD}}=180^{\circ}O1​​+O3​​+AOD=180∘.

Từ $(4)$ và (5) \Rightarrow \widehat{{EOF}}=180^{\circ}(5)⇒EOF=180∘.

Vậy $E,O,F$ nằm trên một đường thẳng, hay tia $OE$ và tia $OF$ là hai tia đối nhau.

Answer 4

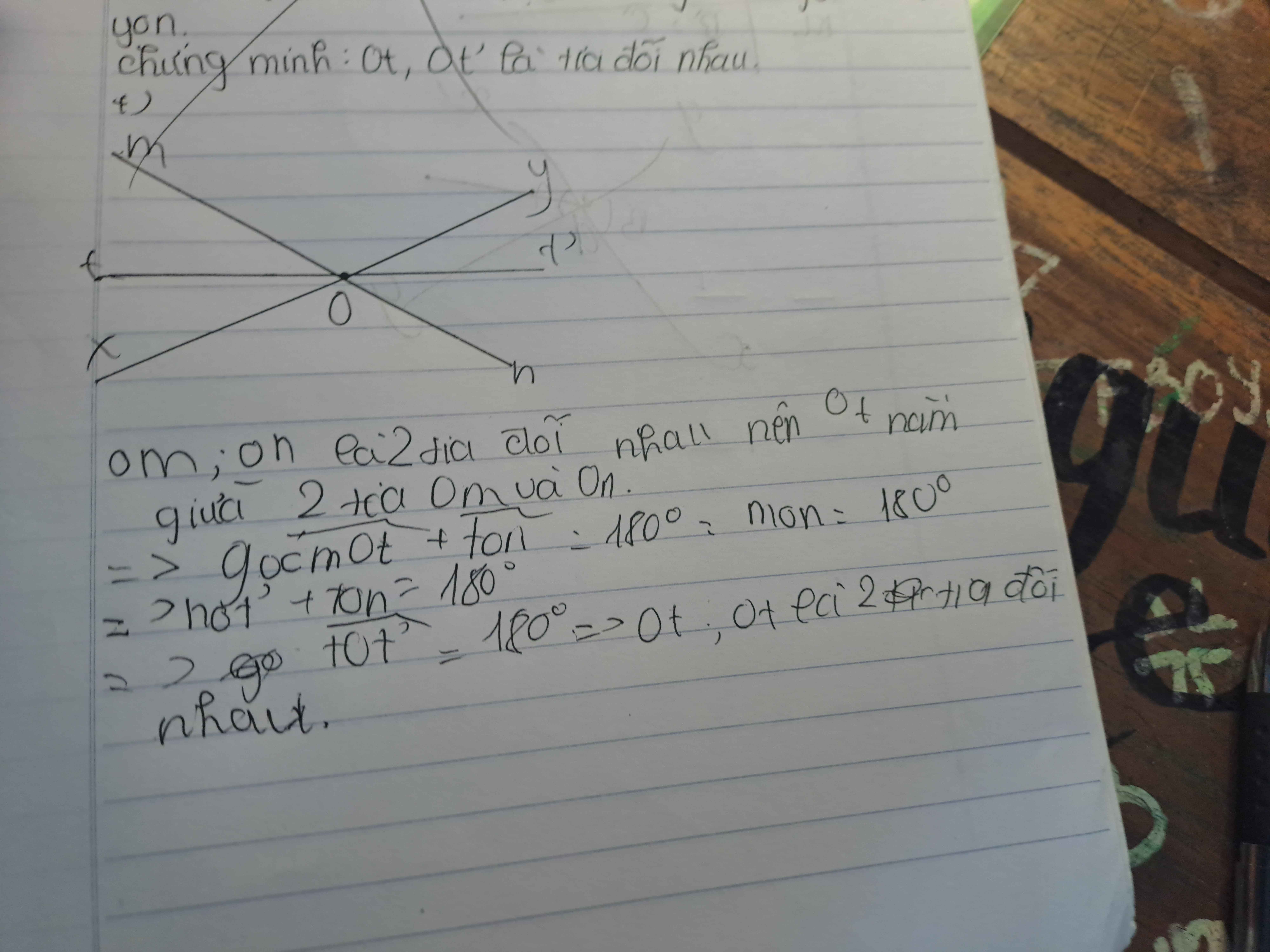
Ta biết: 0C đối OD; OE đối OF => góc COE = góc FOD (2 góc đối đỉnh) (1)

1/2 COE = góc 01 = góc O2 (0a là tia phân giác góc COE) (2)

1/2 FOD = góc 03 = góc O4 (0b là tia phân giác góc FOD) (3)

(1), (2), (3) -> góc 01 = góc 02 = góc 03 = góc 04

Biết: góc 05 = góc 06 (2 góc đối đỉnh) (4)

Vì: góc 05 + góc 6 + góc 1 + góc 2 + góc 03 + góc 04 = 360

hay 2 góc 05+ 2 góc 01 + 2 góc 03 = 360

2 (góc 05 + góc 01 + góc 03) = 360

2 góc a0b=360 -> góc a0b = 180

KL: Tia phân giác 0a đối tia phân giác ob

Answer 5

 

Answer 6

Hai tia phân giác của 2 góc đời đỉnh thì đó là hai tia đối nhau 

Answer 7

Gọi 2 góc đối đỉnh là ab và a`b` ; gọi 2 tia phân giác là c và c`

góc ab = góc a`b` (góc đối đỉnh) (1)

góc ac = góc a`c` = góc bc = góc b`c` ( vì (1) ) (2)

từ (1) và (2) ta suy ra

tia phân giác c và tia phân giác c` là hai tia đối nhau ( góc ĐỐI đỉnh )

 

Answer 8

Vậy E, O, F nằm trên một đường thẳng, hay tia OE và tia OF là hai tia đối nhau.

 

Answer 9

Góc O₁  = góc O₂ ( OE là tia phân giác của góc AOC ) 

Góc O₃ = góc O₄ ( OF là tia phân giác của góc DOB)

Mà góc AOD = góc COB (hai góc đối đỉnh)

Từ 3 biểu thức trên, ta có: Góc O₁ + góc O₃ + góc AOD = góc O₂ + góc O₄ + góc COB

Mà ( góc O₁ + góc O₃ + góc AOD) + ( góc O₂ + góc O₄ + góc COB) = 360 độ

Do đó góc O₁ + góc O₃ +  góc AOD = 180 độ

=> EOF = 180 độ

Vậy E,O,F nằm trên một đường thẳng, hay tia OE và tia OF là hai tia đối nhau.

Answer 10

Vì góc độ đó bằng nhau 

Answer 11