Question

Chứng minh rằng đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm của hai đường chéo và đi qua trung điểm của cạnh bên thứ hai.

Answer 1

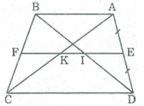
Xét hình thang ABCD có AB // CD.

E là trung điểm AD, đường thẳng đi qua E song song với AB cắt BC tại F, AC tại K, BD tại I.

Vì E là trung điểm AD nên EF// AB

Suy ra: BF = FC (tính chất đường trung bình hình thang)

Trong ∆ ADC ta có: E là trung, điểm của cạnh AD

EK // DC

Suy ra: AK = KC (tính chất đường trung bình của tam giác)

Trong  ∆ ABD ta có: E là trung điểm của cạnh AD

EI // AB

Suy ra: BI = ID (tính chất đường trung bình của tam giác)

Vậy đường thẳng song song với 2 đáy, đi qua trung điểm E của cạnh bên AD của hình thang ABCD thì đi qua trung điểm của cạnh bên BC và trung điểm hai đường chéo AC, BD.