Vì
![]()
nên F(x) và G(x) đều là một nguyên hàm của
![]()
Vì
![]()
nên F(x) và G(x) đều là một nguyên hàm của
![]()
Chứng minh rằng các hàm số F(x) và G(x) sau đều là một nguyên hàm của cùng một hàm số:
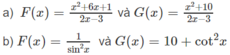
Chứng minh rằng các hàm số F(x) và G(x) sau đều là một nguyên hàm của cùng một hàm số: F x = x 2 + 6 x + 1 2 x - 3 và G x = x 2 + 10 2 x - 3
Giả sử f(x) là hàm số liên tục trên đoạn [a; b], F(x) và G(x) là hai nguyên hàm của f(x). Chứng minh rằng F(b) – F(a) = G(b) – G(a), (tức là hiệu số F(b) – F(a) không phụ thuộc việc chọn nguyên hàm).
Cho hàm số f(x) xác định và liên tục trên R. Gọi g(x) là một nguyên hàm của y= x x + f 2 ( x ) hàm số Biết rằng ∫ 1 2 g ( x ) d x = 1 và 2g(2)-g(1)=2 Tích phân
∫ 1 2 x 2 x + f 2 ( x ) d x bằng
A. 1,5
B. 1
C. 3
D. 2
Cho hai hàm số liên tục f(x) và g(x) có nguyên hàm lần lượt là F(x) và G(x) trên [0; 2]. Biết F(0) = 0, F(2) = 1, G(2) = 1 và ∫ 0 2 F ( x ) g ( x ) d x = 3 . Tính tích phân hàm: ∫ 0 2 G ( x ) f ( x ) d x
A. I = 3.
B. I = 0.
C. I = -2.
D. I = -4.
Biết F(x) là một nguyên hàm của hàm số f(x) = sin x và đồ thị hàm số y = F(x) đi qua điểm M(0;1) . Tính F π 2 .
A. F π 2 = 0
B. F π 2 = 1
C. F π 2 = 2
D. F π 2 = - 1
Trong các hàm số dưới đây, hàm số nào là một nguyên hàm của hàm số f x = 1 1 + sinx
a) F(x) = 1 - cos x 2 + π 4
b) G(x) = 2 tan x 2
c) H(x) = ln(1 + sinx)
d) K(x) = 2 1 - 1 1 + tan x 2
Cho hàm số y = f(x) có đạo hàm f'(x). Hàm số y = f'(x) liên tục trên tập số thực và có bảng biến thiên như sau:
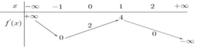
Biết rằng f(-1) = 10 3 , f(2) = 6. Giá trị nhỏ nhất của hàm số g(x) = f 3 ( x ) - 3 f ( x ) trên đoạn [-1;2] bằng
A. 10 3
B. 820 27
C. 730 27
D. 198
Cho hàm số y=f(x) có đạo hàm liên tục trên R và có đồ thị hàm số y=f '(x) như hình vẽ bên dưới. Xét hàm số g(x)=f(x^2-3) và các mệnh đề sau:
I. Hàm số ![]() có 3 điểm cực trị.
có 3 điểm cực trị.
II. Hàm số g(x)đạt cực tiểu tại x=0
III. Hàm số g(x) đạt cực đại tại x=2
IV. Hàm số g(x) đồng biến trên khoảng (-2;0)
V. Hàm số g(x) nghịch biến trên khoảng (-1;1)
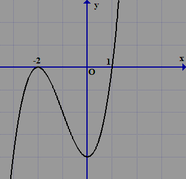
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên?
A.1
B.4
C.3
D.2