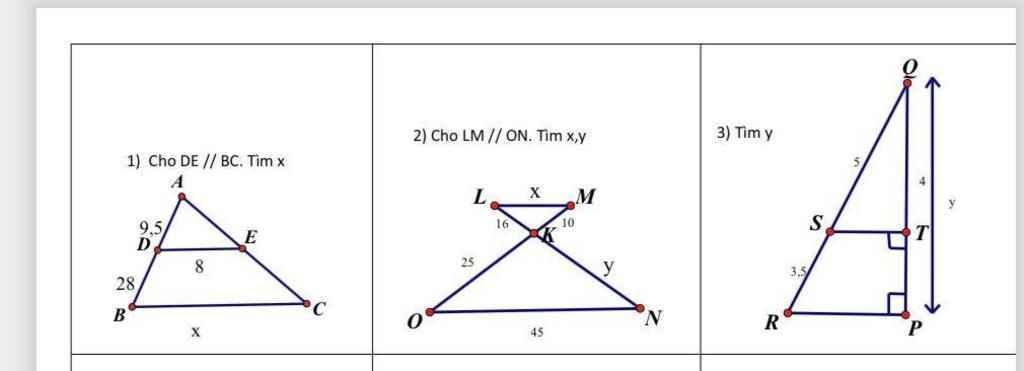
Tam giác ABC có MN // BC (M thuộc AB, N thuộc AC)
S(ACM)/S(ABC) = AM/AB (1)
S(ABN)/S(ABC) = AN/AC (2)
Mà S(ACM) = S(AMN) + S(CMN) (3)
và S(ABN) = S(AMN) + SBMN) (4)
Mặt khác do MNCB hình thang nên dễ dàng chứng minh
S(CMN) = S(BMN) (5)
Từ (3) , (4) và (5) cho:
S(ACM) = S(ABN) (6)
(1) , (2) và (6) cho:
AM/AB = AN/AC (đpcm)
-----------
Cách viết S(ABC) đọc là diện tích tam giác ABC
Giả sử tam giác ABC và DE // BC
Ta cần C/M \(\frac{AB}{AD}=\frac{AC}{AE}=\frac{BC}{DE}\)
Vì DE // BC
=> ^B = ^D1 ( đồng vị )
Xét tam giác ABC và tam giác ADE có :
\(\widehat{A}\)chung
\(\widehat{B}=\widehat{D_1}\)(CMT)
\(\Rightarrow\Delta ABC~\Delta ADE\left(g.g\right)\)(~ là đồng dạng nhé )
\(\Rightarrow\frac{AB}{AD}=\frac{AC}{AE}=\frac{BC}{DE}\)( Đpcm )
Vậy ...
Tam giác ABC có MN // BC ( M thuộc AB, N thuộc AC )
\(\frac{S_{ACM}}{S_{ABC}}=\frac{AM}{AB}\left(1\right)\)
\(\frac{S_{ABN}}{S_{ABC}}=\frac{AN}{AC}\left(2\right)\)
Mà \(S_{ACM}=S_{AMN}+S_{CMN}\left(3\right)\)
và \(S_{ABN}=S_{AMN}+S_{BMN}\left(4\right)\)
Mặt khác do \(MNBC\) hình thang nên dễ dàng chứng minh
\(S_{CMN}=S_{BMN}\left(5\right)\)
Từ (3), (4) và (5) cho:
\(S_{ACM}=S_{ABN}\left(6\right)\)
Từ (1), (2) và (6) cho:
\(\frac{AM}{AB}=\frac{AN}{AC}\left(đpcm\right)\)
Xét \(\Delta ABC\left(MN//BC;M\in AB,N\in AC\right)\)
\(\frac{S_{ACM}}{S_{ABC}}=\frac{AM}{AB}\left(1\right) \)
\(\frac{S_{ABN}}{S_{ABC}}=\frac{AN}{AC}\left(2\right)\)
Mà \(S_{ACM}=S_{AMN}+S_{CMN}\left(3\right)\)
và \(S_{ABN}=S_{AMN}+S_{BMN}\left(4\right)\)
Mặt khác do MNBC là hình thang nên chứng minh được:
\(S_{CMN}=S_{BMN}\left(5\right)\)
Từ (3), (4) và (5) suy ra:
\(S_{ACM}=S_{ABN}\left(6\right)\)
Từ (1), (2) và (6) ta được:
\(\frac{AM}{AB}=\frac{AN}{AC}\left(đpcm\right)\)