Các câu hỏi tương tự
Giả sử
x
a
m
;
y
b
m
(a, b, m ∈ Z; m 0) và x y. Hãy chứng minh nếu chọn
z
a
+
b
2
m
thì ta có x z y. Hướng dẫn: Sử dụng tính chất: Nếu a, b, c ∈ Z và a b thì a + c b...
Đọc tiếp
Giả sử x = a m ; y = b m (a, b, m ∈ Z; m > 0) và x < y. Hãy chứng minh nếu chọn z = a + b 2 m thì ta có x < z < y.
Hướng dẫn: Sử dụng tính chất: Nếu a, b, c ∈ Z và a < b thì a + c < b + c
a, cho 3 số x, y, z có tổng khác 0 thỏa mãn điều kiện \(\frac{x}{y}=\frac{y}{z}=\frac{z}{x}\)
Tính giá trị biểu thức \(M=\frac{x^{670}.y^{670}.z^{670}}{y^{2012}}\)
b, CMR: Nếu a + c = 2b và 2bd = c(b + d) thì \(\frac{a}{b}=\frac{c}{d}\)với b, d khác 0
c, Cho x, y, z là các số khác 0 và x2 = yz; y2 = xz; z2 = xy
CMR: x = y = z
CMR : nếu a( y+z)=b(x+z)=c(x+y) với a,b,c khác nhau và khác 0 . thì
y-z / a(b-c) = z-x / b(c-a) = x-y / c(a-b)
Giả sử x=a/m, y=b/m (a,b,m€Z,m>0) và x<y. Hãy chứng tỏ rằng nếu chọn z=a+b/2m thì ta có x<z<y.
Hướng dẫn sử dụng tính chất nếu a,b,c €Z và a<b thì a+c<b+c.
Giả sử x = a/m ; y = b/m (a, b, m thuộc Z, m < 0) và x > y. Hãy chứng tỏ rằng nếu chọn z = (a + b) / 2m thì ta có x < z < y.
Sử dụng tính chất: Nếu a, b, c thuộc Z và a < b thì a + c < b + c
Giả sử X = a/m , Y=b/m (a,b,m thuộc Z) và x<y. Hãy chứng tỏ rằng nếu chọn z = a+b/2m thì ta có x<z<y
HD: Sử dụng tính chất: Nếu a,b,c thuộc Z và a<b thì a+c<b+c
Bài 20: (Đăng hộ)a, cho 3 số x, y, z có tổng khác 0 thỏa mãn điều kiện frac{x}{y}frac{y}{z}frac{z}{x}Tính giá trị biểu thức M frac{x^{670}.y^{670}.z^{670}}{y^{2012}}b, CMR: Nếu a + c 2b và 2bd c(b + d) thì frac{a}{b}frac{c}{d} với b, d khác 0c, Cho x, y, z là các số khác 0 và x2 yz; y2 xz; z2 xyCMR: x y z
Đọc tiếp
Bài 20: (Đăng hộ)
a, cho 3 số x, y, z có tổng khác 0 thỏa mãn điều kiện \(\frac{x}{y}=\frac{y}{z}=\frac{z}{x}\)
Tính giá trị biểu thức M = \(\frac{x^{670}.y^{670}.z^{670}}{y^{2012}}\)
b, CMR: Nếu a + c = 2b và 2bd = c(b + d) thì \(\frac{a}{b}=\frac{c}{d}\) với b, d khác 0
c, Cho x, y, z là các số khác 0 và x2 = yz; y2 = xz; z2 = xy
CMR: x = y = z
Cho các số a, b, c khác 0. Tính giá trị của biểu thức : \(A=x^{2oo3}+y^{2oo3}+z^{2oo3}.\)
Biết x, y, z thỏa mãn điều kiện \(\frac{x^2+y^2+z^2}{a^2+b^2+c^2}=\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}\)
Chứng minh rằng nếu có : a(y+z) = b(z+x) = c(x+y) . Trong đó a , b , c là các số khác nhau và khác 0 thì y-z / a(b-c) = z-x / b(c-a) = x-y /c(a-b)
Chứng minh rằng nếu có : a(y+z) = b(z+x) c(x+y) . Trong đó a , b , c là các số khác nhau và khác 0 thì : y-z / a(b-c) = z-x / b(c-a) = x-y / c(a-b)




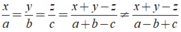 nên D sai
nên D sai







