Chọn C.
Vì Δ = -3 nên phương trình có hai nghiệm phức: ![]() (do z1 có phần ảo dương)
(do z1 có phần ảo dương)
Ta có: 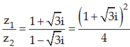
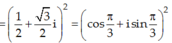
Do đó:
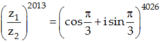
![]()
Vậy phần thực bằng 1, phần ảo bằng 0.
Chọn C.
Vì Δ = -3 nên phương trình có hai nghiệm phức: ![]() (do z1 có phần ảo dương)
(do z1 có phần ảo dương)
Ta có: 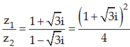
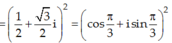
Do đó:
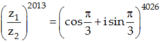
![]()
Vậy phần thực bằng 1, phần ảo bằng 0.
Gọi z 1 , z 2 là hai nghiệm phức của phương trình z 2 + 2z + 5 = 0, trong đó z 1 có phần ảo dương. Tìm số phức liên hợp của số phức z 1 + 2 z 2
A. 3 + i
B. -3 + 2i
C. 3 - 2i
D. 2 - i
Gọi z 1 , z 2 là hai nghiệm phức của phương trình z 2 + 2 z + 5 = 0 , trong đó z 1 có phần ảo dương. Tìm số phức liên hợp của số phức z 1 + 2 z 2
A. 3 + i
B. -3 + 2i
C. 3 - 2i
D. 2 - i
Gọi z1; z2 là hai nghiệm phức của phương trình z2 – z + 1 = 0 . Tìm phần thực, phần ảo của số phức ![]() lần lượt là?
lần lượt là?
A. 0; 1
B. 1; 0
C. -1; 0
D. 0; -1
Cho phương trình 8z2 - 4(a + 1)z + 4a + 1 = 0 (1) với a là tham số. Tính tổng tất cả các giá trị của a để (1) có hai nghiệm z1; z2 thỏa mãn z1/ z2 là số ảo, trong đó z2 là số phức có phần ảo dương.
A. 1
B. 2
C. 3
D. 4
Gọi z1 ; z2 là hai nghiệm của phương trình z2 + 2z+ 8= 0, trong đó z1 có phần ảo dương. Giá trị của số phức ![]() là:
là:
A. 12+ 6i
B. 10
C. 8
D.12- 6i
Biết phương trình a z 3 + b z 2 + c z + d = 0 ( a , b , c , d ∈ R ) có z1, z2, z3 là các nghiệm, biết rằng z3=1+2i là nghiệm của phương trình. Biết z2 có phần ảo âm. Tìm phần ảo của số phức w = z 1 + 2 z 2 + 3 z 3
![]()
![]()
![]()
![]()
Gọi z1 là nghiệm phức có phần ảo dương của phương trình z 2 - 2 z + 5 = 0 . Tìm số phức liên hợp của w = z 1 2 - i
![]()
![]()
![]()
![]()
Gọi z1 là nghiệm phức có phần ảo dương của phương trình z 2 - 2 z + 5 = 0 . Tìm số phức liên hợp của w = z 1 2 - i
![]()
![]()
![]()
![]()
Trong tập các số phức, gọi z 1 , z 2 là hai nghiệm của phương trình z 2 - z + 2017 4 = 0 với z 2 có thành phần ảo dương. Cho số phức z thỏa mãn z - z 1 = 1 . Giá trị nhỏ nhất của P = z - z 2 là
A. 2016 - 1
B. 2017 - 1 2
C. 2016 - 1 2
D. 2017 - 1