Đáp án A
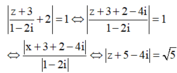
Do đó điểm A biểu diễn số phức z thuộc đường tròn tâm I(-5;4) bán kính R = 5
Số phức w là số thuần ảo nên điểm B biểu diễn w thuộc trục tung
Ta có: ![]()
Đáp án A
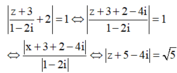
Do đó điểm A biểu diễn số phức z thuộc đường tròn tâm I(-5;4) bán kính R = 5
Số phức w là số thuần ảo nên điểm B biểu diễn w thuộc trục tung
Ta có: ![]()
Cho z và w là các số phức thỏa mãn các điều kiện z w + 1 + i w - 1 = 0 ; w + 2 = 1 . Giá trị nhỏ nhất của biểu thức T = z - 1 - 3 i bằng
A. 2 2
B. 4 2
C. 3 2
D. 5 2
Cho số phức z thỏa mãn |z - 3 - 4i| = 5 . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = | z + 2 | 2 - | z - i | 2 . Tính môđun của số phức w = M + mi ?
A. |w| = 2315
B. |w| = 1258
C. |w| = 3 137
D. |w| = 2 309
Cho các số phức w,z thỏa mãn w + i = 3 5 5 và 5w=(2+i)(z-4).
Giá trị lớn nhất của biểu thức P = z - 1 - 2 i + z - 5 - 2 i bằng
A. 6 7
B. 4 + 2 13
C. 2 53
D. 4 13
Cho các số phức w, z thỏa mãn w + i = 3 5 5 và 5 w = ( 2 + i ) ( z - 4 ) . Giá trị lớn nhất của biểu thức P = z - 1 - 2 i + z - 5 - 2 i bằng
![]()
![]()
![]()
![]()
Cho các số phức w, z thỏa mãn w + i = 3 5 5 và 5 w = 2 + i z - 4 . Giá trị lớn nhất của biểu thức P = z - 1 - 2 i + z - 5 - 2 i bằng
A. 6 7
B. 4 + 2 13
C. 2 53
D. 4 13
Cho số phức z thỏa mãn điều kiện 2 + i z + 1 - i 1 + i = 5 - i . Môđun của số phức w = 1 + 2 z + z 2 có giá trị là
A. 10.
B. 25
C. 100.
D. 40
Cho số phức z thỏa mãn điều kiện 2 + i z + 1 - i 1 + i = 5 - i Môđun của số phức w = 1 + 2 z + z 2 có giá trị là
A. -10
B. 100
C. -100
D. 10
Cho số phức z thỏa mãn điều kiện ( 3 + 2 i ) z + ( 2 - i ) 2 = 4 + i . Tìm phần ảo của số phức w = ( 1 + z ) z ¯ .
![]()
![]()
![]()
![]()
Cho số phức z thỏa mãn điều kiện (z+2)(1+2i) = 5 z ¯ . Tìm phần ảo của số phức w = ( z + 2 i ) 2019
A . 2 1009
B . 0
C . - 2 1009
D . 2019