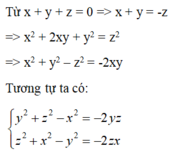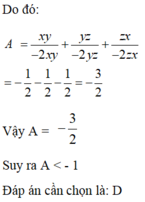Các câu hỏi tương tự
1)cho 3 số x, y,z thỏa mãn điều kiện x+y+z=2018 và x^3+y^3+z^3=2018^3. Cmr (x+y+z)^3=x^2017+y^2017+z^2017
2)
tìm các cặp số nguyên (x y) biết x^2-4xy+5y^2-16=0
3)Cho 3 số a,b,c thỏa mãn a+b+c=0 và a^2+b^2+c^2=2018
4)tính giả trị biểu thức A=a^4+b^4+c^4
1, Phân tích thành nhân tử: 8(x + y + z)^2 - (x + y)^3 - (y + z)^3 - (z + x)^32, a, Phân tích thành nhân tử: 2x^2y^2 + 2y^2z^2 + 2z^2x^2 - x^4 - y^4 - z^4b, Chứng minh rằng nếu x, y, x là ba cạnh của 1 tam giác thì A 03, Cho x, y, x là độ dài 3 cạnh của một tam giác ABC. Chứng minh rằng nếu x, y, z thỏa mãn các đẳng thức sau thì tam giác ABC là tam giác đều:a, (x + y+ z)^2 3(xy + yz + zx)b, (x + y)(y + z)(z + x) 8xyzc, (x - y)^2 + (y - z)^2 + (z - x)^2 (x + y - 2z)^2 + (y + z - 2x)^2 + (z +...
Đọc tiếp
1, Phân tích thành nhân tử: 8(x + y + z)^2 - (x + y)^3 - (y + z)^3 - (z + x)^3
2,
a, Phân tích thành nhân tử: 2x^2y^2 + 2y^2z^2 + 2z^2x^2 - x^4 - y^4 - z^4
b, Chứng minh rằng nếu x, y, x là ba cạnh của 1 tam giác thì A > 0
3, Cho x, y, x là độ dài 3 cạnh của một tam giác ABC. Chứng minh rằng nếu x, y, z thỏa mãn các đẳng thức sau thì tam giác ABC là tam giác đều:
a, (x + y+ z)^2 = 3(xy + yz + zx)
b, (x + y)(y + z)(z + x) = 8xyz
c, (x - y)^2 + (y - z)^2 + (z - x)^2 = (x + y - 2z)^2 + (y + z - 2x)^2 + (z + x - 2y)^2
d, (1 + x/z)(1 + z/y)(1 + y/x) = 8
4,
a, Cho 3 số a, b, c thỏa mãn b < c; abc < 0; a + c = 0. Hãy so sánh (a + b - c)(b + c - a)(c + a -b) và (c - b)(b - a)(a - c)
b, Cho x, y, z, t là các số nguyên dương thỏa mãn x + z = y + t; xz 1 = yt. Chứng minh y = t và x, y, z là 3 số nguyên liên tiếp
5, Chứng minh rằng mọi x, y, z thuộc Z thì giá trị của các đa thức sau là 1 số chính phương
a, A = (x + y)(x + 2y)(x + 3y)(x + 4y) + y^4
b, B = (xy + yz + zx)^2 + (x + y + z)^2 . (x^2 + y^2 + z^2)
Bài 1: Cho x,y,z khác 0 và x+y+z0Tính giá trị của biểu thức1/y2 + z2 - x2 + 1/x2 + y2 - z2 + 1/x2+z2 - y2Bài 2: Cho x,y,z khác 0 và 1/x - 1/y - 1/z 1 và xy+zCMR 1/x + 1/y +1/z 1Bài 3: Cho a,b,c khác 0 và x2+y2+z2/a2+b2+c2 x2/a2 + y2/b2 +z2/c2CMR: xyz0Bài 4: Cho các số a,b,c thỏa mãn:a+b+c1a2 + b2 +c21 và x/ay/bz/cCMR: xy+yz+xz0
Đọc tiếp
Bài 1: Cho x,y,z khác 0 và x+y+z=0
Tính giá trị của biểu thức
1/y2 + z2 - x2 + 1/x2 + y2 - z2 + 1/x2+z2 - y2
Bài 2: Cho x,y,z khác 0 và 1/x - 1/y - 1/z =1 và x=y+z
CMR 1/x + 1/y +1/z =1
Bài 3: Cho a,b,c khác 0 và x2+y2+z2/a2+b2+c2 = x2/a2 + y2/b2 +z2/c2
CMR: x=y=z=0
Bài 4: Cho các số a,b,c thỏa mãn:
a+b+c=1
a2 + b2 +c2=1 và x/a=y/b=z/c
CMR: xy+yz+xz=0
cho `x,y,z` khác `0` thỏa mãn `x + y/2 + z/3 = 1` và `1/x + 2/y + 3/z =0`. Chứng tỏ `A= x^2 + (y^2)/4 + (z^2)/9 =1`
cho x,y,z khác 0 và x khác y khác z , thỏa mãn :
x^2 -xy = y^2-yz = z^2 - zx = a
1 ) cmr : a khác 0
2) cmr ; 1/x + 1/y + 1/z = 0
3 ) tính M = x/z + z/y + y /x
Cho các số a,b,c,x,y,z khác 0 và thỏa mãn \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1\) và \(\frac{a}{x}+\frac{b}{y}+\frac{c}{z}=0\)
Tính giá trị biểu thức: \(A=\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}\)
1.cho x > 0. tìm GTNN của A = \(\dfrac{3x^4+16}{x^3}\)
2. cho x,y,z > 0 thỏa mãn x+y+z=2. tìm GTNN của biểu thức:
P=\(\dfrac{x^2}{y+z}+\dfrac{y^2}{z+x}+\dfrac{z^2}{x+y}\)
giúp mình với ạ, mình đang cần gấp trong tối nay ạ.
cho x ,y,z khác 0 thỏa mãn x+y+z=0 Tính giá trị của biểu thức M=\(\frac{1}{x^2+y^2-z^2}+\frac{1}{y^2+z^2-x^2}+\frac{1}{x^2+z^2-y^2}\)
a,Cho a2+b2+(a+b)2c2+d2+(c+d)2. CM: a4+b4+(a+b)4c4+d4+(c+d)4b, Cho x,y,z là các số thực thỏa mãn: (x-y)2 + (y-z)2 + (z-x)2 (x+y-2z)2 + (y+z-2x)2 + (x+z-2y)2. CM: xyzc, Cho x, y là các số thỏa mãn: 2x2 +y3 - 4x + 3 0 và x2y2 + y2 - 2x0. Tính giá trị biểu thức A x100y1001 + x700y2d, Cho x, y, z thỏa mãn (x+y+z)3 - x3 -y3 -z3 0. Tính giá trị biểu thức: P (x2015 + y2015 )(y2017+ z2017)(z2019+x2019)
Đọc tiếp
a,Cho a2+b2+(a+b)2=c2+d2+(c+d)2. CM: a4+b4+(a+b)4=c4+d4+(c+d)4
b, Cho x,y,z là các số thực thỏa mãn: (x-y)2 + (y-z)2 + (z-x)2 = (x+y-2z)2 + (y+z-2x)2 + (x+z-2y)2. CM: x=y=z
c, Cho x, y là các số thỏa mãn: 2x2 +y3 - 4x + 3 = 0 và x2y2 + y2 - 2x=0. Tính giá trị biểu thức A= x100y1001 + x700y2
d, Cho x, y, z thỏa mãn (x+y+z)3 - x3 -y3 -z3 = 0. Tính giá trị biểu thức: P = (x2015 + y2015 )(y2017+ z2017)(z2019+x2019)
Cho x,y,z khác 0 và A=y/z+z/y;B=x/z+z/x;C=x/y+y/x.Tính giá trị biểu thức: A^2+B^2 +C^2-A*B*C