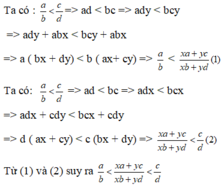Các câu hỏi tương tự
cho các số hữu tỉ x=a/b,y=c/d. z=a+c/b+d(a,b,c,d thuộc Z;b,d >0).Chứng minh rằng nếu x<y thì x<z<y
15 tháng 9 2019 lúc 20:41
Cho các số hữu tỉ: x = a/b; y = c/d; z = a+c/b+d ( a, b, c, d \(\in\)Z; b > 0, d > 0)
Chứng minh rằng nếu x < y thì x < z < y
Chứng minh rằng nếu a + b/ b+ c = c+ d/ d+ a thì a= c hoặc a+ b+ c+ d= 0 (với c+ d# 0)Cho x/a+2b+c= y/2a+y-z = z/4a-4b+c. Chứng minh rằng : a/x+2y+z=b/ 2x+y-z = c/ 4x- 4y+ c
Xem chi tiết
( với abc # 0 và các mẫu đều khác 0)
Chứng mình rằng , nếu x<y thì x<z<y
Biết x=a/b , y=c/d , z=a+c/b+d (a,b,c,d thuộc Z , b>d>0)
Cho x = a/b, y = c/d, z = a+c/b+d (a, b, c,d thuộc Z; b, d >0). Chứng tỏ rằng nếu x<y thì x<z<y
1) Cho a/b = c/d với b , d khác 0 , b khác +- d chứng minh a/b = c/d = a+c/ b+d = a-c/b-d
2) Cho x/3 = y/5 và x+y = 16
Tìm x , y
Toán nâng cao:
a) Cho a/b = c/d. Chứng minh: a/3a + b = c/3c + d
b) Cho a/b = c/d. Chứng minh rằng: (a - b)2/(c - d)2 = ab/cd
c) Tìm x, y, z biết: x/3 = y/7 = z/2 và 2x2 + y2 + 3z2 = 316
Câu 1:Cho các số hữu tỉ x =a/b; y = c/d ; z = m/n. Biết ad-bc = 1; cn - dm = 1 ; b,d,n > 0
a) Hãy so sánh các số x,y,z
b) So sánh y với t biết t = a+m /b+n với b+n khác 0
Câu 2: Cho 6 số nguyên dương a<b<c<d<m<n
Chứng minh rằng a+c+m / a+b+c+d+m+n < 1/2.
cho các số hữu tỉ x=a/b; y= c/d ; b > 0 ; d< 0 và các số tự nhiên m,n với m # 0 . chứng minh rằng: nếu a/b < c/d thì a/b < ma + nc / mb + nd < c/d
+) cho x=y/2;y/3=z/4. tính x+y+z/x+y-z
+)cho ad=bc với c,d khác 0 ,c khác d. chứng minh (a-b/c-d)^2007=a^2007-b^2007/c^2007-d^2007