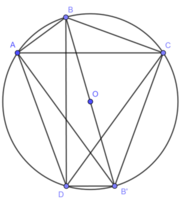
Kẻ đường kính BB’. Nối B’A, B’D, B’C.
Ta có: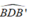 = 90° ( góc nội tiếp chắn nửa đường tròn)
= 90° ( góc nội tiếp chắn nửa đường tròn)
⇒ AC // B'D ( cùng vuông góc với BD)
Suy ra, tứ giác ADB’C là hình thang
Vì ADB’C nội tiếp đường tròn (O) nên ADB’C là hình thang cân
⇒ CD = AB'
⇒ A B 2 + C D 2 = A B 2 + A B ' 2
Mà tam giác BAB’ vuông tại A do 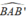 = 90° ( góc nội tiếp chắn nửa đường tròn)
= 90° ( góc nội tiếp chắn nửa đường tròn)
⇒ A B 2 + C D 2 = A B 2 + A B ' 2 = 2 R 2 = 4 R 2 (đpcm)











