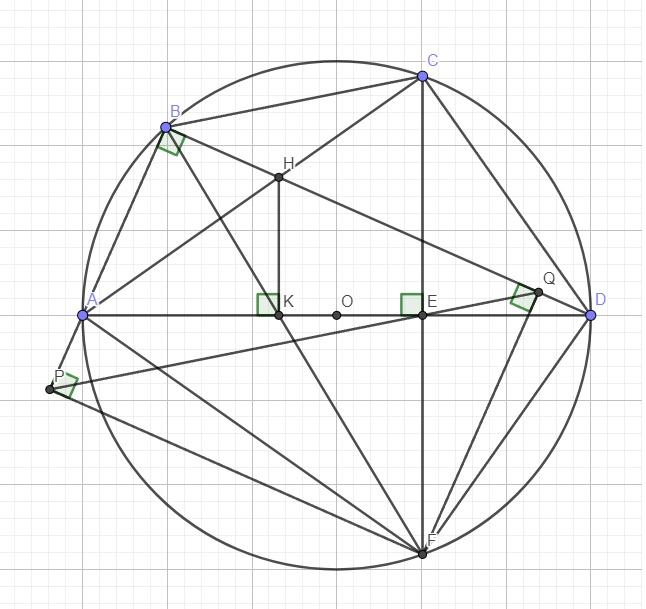
Cho tứ giác ABCD nội tiếp đường tròn (O) đường kính AD (B thuộc cung nhỏ AC). Gọi giao điểm hai đường chéo AC và BD là H. Kẻ HK vuông góc với AD tại K. Tia BK cắt (O) tại điểm thứ hai là F. Gọi P, Q lần lượt là hình chiếu vuông góc của F trên các đường thẳng AB, BD. Chứng minh CF//HK và PQ đi qua trung điểm của CF.
Do AD là đường kính \(\Rightarrow\widehat{ABD}=90^0\) (góc nt chắn nửa đường tròn)
\(\Rightarrow B,K\) cùng nhìn AH dưới 1 góc vuông nên ABHK nội tiếp
\(\Rightarrow\widehat{ABK}=\widehat{AHK}\) (cùng chắn AK)
Mà \(\widehat{ABK}=\widehat{ACF}\) (cùng chắn AF của (O))
\(\Rightarrow\widehat{AHK}=\widehat{ACF}\)
\(\Rightarrow CF||HK\) (hai góc đồng vị bằng nhau)
\(\Rightarrow CF\perp AD\)
Gọi E là giao điểm của CF và AD \(\Rightarrow E\) là trung điểm CF (tính chất đường kính vuông góc dây cung)
Ta có E và P cùng nhìn AF dưới 1 góc vuông \(\Rightarrow AEFP\) nội tiếp
\(\Rightarrow\widehat{PEF}=\widehat{PAF}\) (cùng chắn PF)
ABDF nội tiếp (O) \(\Rightarrow\widehat{BAF}+\widehat{QDF}=180^0\)
Mà \(\widehat{BAF}+\widehat{PAF}=180^0\) (kề bù)
\(\Rightarrow\widehat{PEF}=\widehat{QDF}\) (1)
E và Q cùng nhìn DF dưới 1 góc vuông \(\Rightarrow EQDF\) nội tiếp
\(\Rightarrow\widehat{QEF}+\widehat{QDF}=180^0\) (2)
(1);(2) \(\Rightarrow\widehat{PEF}+\widehat{QEF}=180^0\)
\(\Rightarrow P,E,Q\) thẳng hàng hay PQ đi qua trung điểm E của CF