Các câu hỏi tương tự
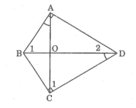
Cho tứ giác ABCD có 2 đường chéo AC, BD vuông góc với nhau tại O và góc BAC = góc BDC. Kẻ OK vuông góc với CD tại K. Đường thẳng OK cắt AB tại I.CMR:
a)IA=IB
b)góc CAD = góc CBD
Cho tứ giác lồi ABCD có hai đường chéo AC và BD vuông góc với nhau và cắt nhau
tại O. Biết rằng BAC=BDC . Từ O kẻ đường thẳng vuông góc với CD cắt AB tại I .
Chứng minh I là trung điểm AB
Cho tứ giác ABCD, AD vuông góc với BD tại O. Biết góc BAC=góc BDC. Kẻ OK vuông góc với CD. Đường thẳng OK cắt AB tại I. C/m: IA=IB
Cho tứ giác ABCD , có hai đường chéo AC và BD vuông góc với nhau và cắt nhau tại O . Từ O kẽ OK vuông góc DC ; OK kéo dài cắt AB ở I . Chứng minh rằng nếu: BAC = BDC thì IA = IB và ngược lại.
Cho hình chữ nhật ABCD (ABAD). Trên cạnh AD,BC lần lượt lấy các điểm M, N sao cho AMCNA) CHỨNG MINH RẰNG BM//DNB) Gọi O là trung điểm của BD. CHỨNG MINH AC, BD, MN đồng quy tại OC) Qua O vẽ đường thẳng d vuông góc với BD, d cắt AB tại P, cắt CD tại Q. CHỨNG MINH: Tứ giác PBQD là hình thoiD) Đường thẳng qua B song song với PQ và đường thẳng qua Q song song với BD cắt nhau tại K. CHỨNG MINH: Tứ giác OBKQ là hình chữ nhật và BC _|_(vuông góc ) OK
Đọc tiếp
Cho hình chữ nhật ABCD (AB>AD). Trên cạnh AD,BC lần lượt lấy các điểm M, N sao cho AM=CN
A) CHỨNG MINH RẰNG BM//DN
B) Gọi O là trung điểm của BD. CHỨNG MINH AC, BD, MN đồng quy tại O
C) Qua O vẽ đường thẳng d vuông góc với BD, d cắt AB tại P, cắt CD tại Q. CHỨNG MINH: Tứ giác PBQD là hình thoi
D) Đường thẳng qua B song song với PQ và đường thẳng qua Q song song với BD cắt nhau tại K. CHỨNG MINH: Tứ giác OBKQ là hình chữ nhật và BC _|_(vuông góc ) OK
Cho hình thoi abcdcos 2 đường chéo ac và bd cắt nhau tại o.kẻ oe vuông góc ab of vuông góc bc oh vuông góc cd ok vuông góc da a) chứng minh oe=of.= oh.= ok b) chứng minh 3 điểm e,o,h thẳng hàng
Cho hình thang ABCD (AB//CD). Gọi O là giao điểm hai đường chéo AC và BD. Đường thẳng qua O vuông góc với AB và CD lần lượt tại H và K. Chứng minh OH/OK = AB/CD
Tứ giác ABCD có hai góc vuông tại đỉnh A và C hai đường chéo AC và BD cắt nhau tại O, ∠ (BAO) = ∠ (BDC) .Chứng minh: △ ABO đồng dạng △ DCO
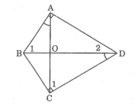
Tứ giác ABCD có hai góc vuông tại đỉnh A và C hai đường chéo AC và BD cắt nhau tại O,
∠
(BAO)
∠
(BDC) .Chứng minh:
△
BCO đồng dạng
△
ADO
Đọc tiếp
Tứ giác ABCD có hai góc vuông tại đỉnh A và C hai đường chéo AC và BD cắt nhau tại O, ∠ (BAO) = ∠ (BDC) .Chứng minh: △ BCO đồng dạng △ ADO