Các câu hỏi tương tự
Cho tam giác đều ABC có cạnh a , I là trung điểm AB , G là trọng tâm , M ,N lần lượt thuộc AB , AC sao cho vt MA + 2. vt MB = vt 0 , vt AN = -2. vt CN. Tính vt MG , vt MN theo vt AB , vt AC , từ đó suy ra M , N , G thẳng hàng
Cho hình bình hành ABCD tâm O. Gọi M, N lần lượt là trung điểm của BC, CD; G là trọng tâm tam giác ABC.
a) Chứng minh AM + AN = 3/2 AC và GA +3GB+GC+GD=0
c) Gọi I là điểm thỏa mãn AI= 3/4AB. Phân tích IN ; IG theo hai vec tơ BA và BC
Chứng minh 3 điểm N;G;I thẳng hàng.
Cho tam giác ABC . Gọi M , N , P là 3 điểm thoả mãn vecto MC = 1/3 vecto MB , vecto NA + 3 vecto NC = 0 , vecto PA + vecto PB = 0 a ) Biểu diễn vecto MP , vecto NP theo hai vecto AB và AC b ) Chứng minh 3 điểm M , N, P thẳng hàng
Cho tam giác ABC có trọng tâm G . Gọi I là trung điểm CG và M,N là các điểm thỏa mãn vectơ MN = vectơ MA + vectơ MB + 4 vectơ MC . Chứng minh rằng 3 điểm M, I , N thẳng hàng.
Cho tam giác ABC, A(4;0) B(2;-4) C(0;-2). Gọi G là trọng tâm tam giác ABC. GỌi M, N, P lần lượt là trung điểm các cạnh BC, CA, AB. Chứng minh tam giác ABC, tam giác MNP có cùng trọng tâm
cho tam giác ABC gọi G là trọng tâm cuả tam giác ; I là điểm xác định bởi →IA+2*→IB=→0; j là điểm trên BC sao cho →JB=x* →JC
a,biểu diễn →CI, →CJ theo →CA, →CB
b,biểu diễn→IJ theo →CA và →CB
c,tìm x để IJ//CG
Cho hình bình hành ABCD. Gọi M, N là các điểm nằm trên các cạnh AB và CD sao cho AM AB, CN CD. Gọi G là trọng tâm của tam giác BMN. Hãy phân tích theo hai vecto .
Đọc tiếp
Cho hình bình hành ABCD. Gọi M, N là các điểm nằm trên các cạnh AB và CD sao cho AM = 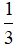
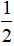
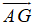
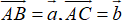
1.cho tam giác ABC gọi K là điểm đối xứng của trọng tâm G qua B.
a. Chứng minh KA-5KB +KC=0 ( đều là vecto hết )
b. Tính vecto AB và AC theo hai vecto AG và AK
cho tam giac ABC có trọng tâm G và M là điểm thỏa mãn MA+4MB=0.xác định điểm N trên cạnh AC sao cho M,N,G thẳng hàng










