Question

Cho tứ giác ABCD có hai đường chéo AC và BD vuông góc với nhau. Biết AC = 6cm, BD = 8cm. Gọi M, N, P, Q theo thứ tự là trung điểm các cạnh AB, BC, CD, DA. Gọi X, Y, Z, T theo thứ tự là trung điểm các cạnh MN, NP, PQ, QM. Chứng minh rằng MNPQ là hình chữ nhật.

Answer 1

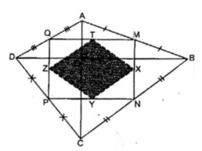
Trong  △ ABD ta có:

M là trung điểm của AB

Q là trung điểm của AD nên MQ là đường trung bình của  △ ABD.

⇒ MQ // BD và MQ = 1/2 BD (tính chất đường trung bình của tam giác) (1)

Trong  △ CBD ta có:

N là trung điểm của BC

P là trung điểm của CD

nên NP là đường trung bình của  △ CBD

⇒ NP // BD và NP = 1/2 BD (tính chất đường trung bình của tam giác) (2)

Từ (1) và (2) suy ra: MQ // NP và MQ = NP nên tứ giác MNPQ là hình bình hành

AC ⊥ BD (gt)

MQ // BD

Suy ra: AC ⊥ MQ

Trong △ ABC có MN là đường trung bình ⇒ MN // AC

Suy ra: MN ⊥ MQ hay (NMQ) = 90 0

Vậy tứ giác MNPQ là hình chữ nhật.