Áp dụng định lý Pytago cho ∆ ABD vuông tại A ta có:

Theo đề bài ta có:
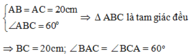
Lại có: AC = AD = 20cm => ∆ ACD cân tại A

Xét BED vuông tại E ta có:
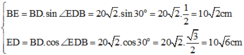
Đáp án cần chọn là: A
Áp dụng định lý Pytago cho ∆ ABD vuông tại A ta có:

Theo đề bài ta có:
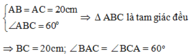
Lại có: AC = AD = 20cm => ∆ ACD cân tại A

Xét BED vuông tại E ta có:
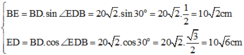
Đáp án cần chọn là: A
Cho tứ giác lồi ABCD có AB=AC=AD=10 cm , góc B bằng 60 độ và góc A là 90 độ .
a. Tính BD
b. Tính khoảng cách BH và DK từ B và D đến AC
c. Tính HK
d. Vẽ BE
e. Vẽ BE vuông góc DC kéo dài . Tính BE,CE và DC
Cho tứ giác lồi ABCD có AB= AC= AD=10 cm , góc B bằng 60 độ và góc A là 90 độ
a) Tính đường chéo BD
b) Tính các khoảng cách BH và DK từ B và D đến AC
c) Tính HK
d) VẼ BE vuông DC kéo dài . Tính BE, CE và DC
Cho tứ giác lồi ABCD có AB = AC = AD = 10cm, góc B = 60 độ và góc A = 90 độ.
a, Tính BD
b, Tính các khoảng cách BH và DK từ B và D đến AC
c, Tính HK
d, Vẽ BE vuông góc với DC kéo dài. Tính BE, CE và DC
Cho tam giác ABC vuông tại A, kẻ đường cao AH và phân giác BE (H thuộc BC, E thuộc AC) Kẻ AD vuông góc BE ( D thuộc BE)
a) CM ADHB nội tiếp trong 1 đường tròn. Xác định tâm O của đường tròn đó
b) CM \(\widehat{EAD}\)= \(\widehat{HBD}\)và OD // HB
c) biết góc ABC=60 độ , và AB = a ( a>0) Tính theo a phần diện tích tam giác ABC nằm ngoài đường tròn O
Làm nốt cho mình phần b với c ạ
Cho hình thang ABCD (AB//CD) góc A =90 độ, góc B=30 độ
a) Cm diện tính hình thang ABCD=1/4 BC(AB+CD)
b) Cho BC giao AD tại E. AK vuông góc với BE (K thuộc BE) KL vuông góc với DE( L thuộc DE). CM 4.AL.AE= AB mũ 2
c) BC=8cm, S tứ giác ABCD= 48 cm2.tính BE, AE
Cho tam giác ABC vuông tại A, kẻ đường cao AH và đường phân giác BE ( H thuộc BC, E thuộc AC). Kẻ AD vuông góc với BE ( D thuộc BE).
a. Chứng minh tứ giác ADHB nội tiếp được trong một đường tròn, xác định tâm O của đường tròn này.
b. Chứng minh tứ giác ODCB là hình thang.
c. Cho biết góc ABC bằng 600, AB có độ dài bằng a. Tính theo a diện tích hình phẳng giới hạn bởi các đoạn AC, BC và cung nhỏ AH của (O).
Cho tam giác ABC vuông cân ở A,trên cạnh AB lấy D, trên AC lấy E sao cho AD=AE. Từ C kẻ đường vuông góc với BE cắt AB ở I
a) CM: BE=IC
b) Qua D và A vẽ đường vuông góc với BE cắt BC tại M và N . CM: MN=CN
Cho tam giác ABC vuông tại A. Từ trung điểm E của AC kẻ EF vuông góc BC.
a) CM: AF = BE. cos C
b) AF giao BE tại O. Biết BC = 10 cm, sin C = 0,6. Tính diện tích tứ giác ABFE và sin AOB.
Cho tam giác ABC vuông tại A, kẻ đường cao AH và đường phân giác BE ( H thuộc BC, E thuộc AC), kẻ AD vuông góc với BE( D thuộc BE).
a. Chứng minh tứ giác ADHB nội tiếp được trong một đường tròn, xác định tâm O của đường tròn này.
b. Chứng minh tứ giác ODCB là hình thang.
c. Cho biết góc ABC có số đo bằng 600, AB có độ dài bằng a. Tính theo a diện tích hình phẳng giới hạn bời các đoạn thẳng AC, BC và cung nhỏ AH của (O).