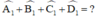Question

Cho tứ giác ABCD có  = 6 : 5 : 4 : 3. Tính các góc của tứ giác ABCD.

b) Cho tứ giác ABCD có  = 60⁰,  = 120⁰,  = 80⁰. Tính số đo góc ngoài tại đỉnh A.

c) Tính tổng các góc ngoài của tứ giác.

d) Chứng minh rằng các góc của tứ giác không thể đều là góc nhọn, không thể đều là góc tù.

Answer 1

a) Tự áp dụng tính chất dãy tỉ số bằng nhau ta có : 

A = 120° 

B = 100° 

C = 80° 

D = 60°

b) Xét tứ giác ABCD có : 

A + B + C + D = 360° 

=> A = 360° - 60° - 120° - 80°= 100° 

Góc ngoài tại A : 

180° - 100° = 80° 

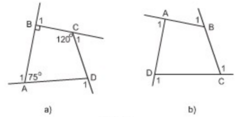
c) Tổng quát : 

Gọi góc ngoài tại A là HAD 

Góc ngoài tại D là ADE

Góc ngoài tại B là CBG 

Góc ngoài tại C là BCM 

Ta có : 

HAD = 180° - DAB 

ADE = 180° ADC 

CBG = 180° - ABC 

BCM = 180° - BCD 

=> HAD + ADE + CBG + BCM =

( 180° - DAB ) + ( 180° - ADC ) + ( 180° - ABC ) + ( 180° - BCD )

= ( 180° + 180° + 180° + 180°) - ( DAB + ACD + ABC + BCD ) 

= 720° - 360° 

= 360° 

=> Tổng các góc ngoài = 360° 

d ) Nếu các góc trong tứ giác  \(\le\)90°

=> Tổng 4 góc trong tứ giác đó sẽ \(\le\)360°

=> Không tồn tại tứ giác đều là góc nhọn 

Nếu các góc trong tứ giác \(\ge\)90° 

=> Tổng các góc trong tứ giác đó \(\ge\)360° 

=> Không tồn tại tứ giác đều là góc tù