Question

cho tứ giác ABCD . chứng minh \(\frac{AB+BC+CD+DA}{2}\) < AC+BD < AB+BC+CD+DA

Answer 1

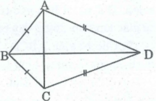
+ AB+BC+CD+DA > AC+BD

Tam giác ABC có: AB + BC > AC (bất đẳng thức tam giác)
Tam giác BCD có BC + CD > BD
Tam giác CDA có CD + DA > AC
Tam giác DAB có DA + AB > BD
=> AB+BC+BC+CD+CD+DA+DA+AB > AC+BD+AC+BD
=> 2(AB+BC+CD+DA) > 2(AC+BD)
=> AB+BC+CD+DA > AC+BD

+AB+BC+CD+DA < 2(AC+BD).
Gọi O là giao điểm của AC và BD
Tam giác OAB có: OA + OB > AB (bất đẳng thức tam giác)
Tam giác OBC có: OB + OC > BC
Tam giác OCD có:OC + OD > CD
Tam giác ODA có: OD +OA > AD

=> OA+OB+OB+OC+OC+OD+OD+OA>AB+BC+CD+DA
=> 2(OA+OC) + 2(OB+OD) > AB+BC+CD+DA
=> 2AC + 2BD  > AB+BC+CD+DA 
=> ( AB+BC+CD+DA)/2 < AC + BD