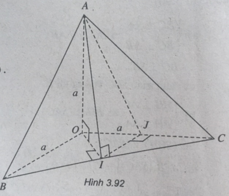
a) (BC ⊥ OA & BC ⊥ OI ⇒ BC ⊥ (OAI)
⇒ (ABC) ⊥ (OAI).
b) + Xác định góc α giữa AB và mặt phẳng (AOI)
(A ∈ (OAI) & BI ⊥ (OAI) ⇒ ∠[(AB,(OAI))] = ∠(BAI) = α.
+ Tính α:
Trong tam giác vuông BAI, ta có: sinα = 1/2 ⇒ α = 30o.
c) Xác định góc β giữa hai đường thẳng AI và OB:
Gọi J là trung điểm OC,
ta có: IJ // OB và IJ ⊥ (AOC). Như vậy:
∠[(AB,OB)] = ∠[(AI,IJ)] = ∠(AIJ) = β.
+ Tính góc:
Trong tam giác IJA,
ta có: tan β = AJ/IJ = √5 ⇒ β = arctan√5.