Các câu hỏi tương tự
Cho tứ diện đều ABCD có cạnh bằng 4. Tính diện tích xung quanh
S
x
q
của hình trụ có một đường tròn đáy là đường tròn nội tiếp tam giác BCD và chiều cao của hình trụ bằng chiều cao của tứ diện ABCD A.
S
x
q
16...
Đọc tiếp
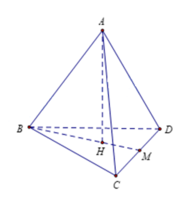
Cho tứ diện đều ABCD có cạnh bằng 4. Tính diện tích xung quanh S x q của hình trụ có một đường tròn đáy là đường tròn nội tiếp tam giác BCD và chiều cao của hình trụ bằng chiều cao của tứ diện ABCD
A. S x q = 16 2 π 3
B. S x q = 8 2 π
C. S x q = 16 3 π 3
D. S x q = 8 3 π
Cho tứ diện đều ABCD cạnh bằng a. Diện tích xung quanh
S
x
q
của hình trụ có đáy là đường tròn ngoại tiếp tam giác BCD và có chiều cao bằng chiều cao của tứ diện ABCD là
Đọc tiếp
Cho tứ diện đều ABCD cạnh bằng a. Diện tích xung quanh S x q của hình trụ có đáy là đường tròn ngoại tiếp tam giác BCD và có chiều cao bằng chiều cao của tứ diện ABCD là
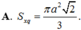
![]()
![]()
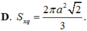
Cho tứ diện ABCD cạnh a. Diện tích xung quanh hình trụ có đáy là đường tròn ngoại tiếp tam giác BCD và có chiều cao bằng chiếu cao tứ diện ABCD là:
Đọc tiếp
Cho tứ diện ABCD cạnh a. Diện tích xung quanh hình trụ có đáy là đường tròn ngoại tiếp tam giác BCD và có chiều cao bằng chiếu cao tứ diện ABCD là:
![]()
![]()
![]()
![]()
Cho tứ diện đều ABCD cạnh a. Gọi H là hình chiếu vuông góc của đỉnh A xuống mặt phẳng (BCD).
Tính diện tích xung quanh của hình trụ và thể tích của khối trụ có đường tròn đáy ngoại tiếp tam giác BCD và chiều cao AH.
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng 3. Tính diện tích xung quanh của hình nón có đáy là đường tròn ngoại tiếp tứ giác ABCD và chiều cao bằng chiều cao của hình chóp.
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng 3. Tính diện tích xung quanh của hình nón có đáy là đường tròn ngoại tiếp tứ giác ABCD và chiều cao bằng chiều cao của hình chóp.
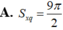
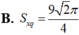
![]()
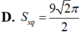
Cho tứ diện đều
A
B
C
D
có cạnh bằng
3
a
. Hình nón
(
N
)
có đỉnh
A
và đường tròn đáy là đường tròn ngoại tiếp tam giác
B
C
D
. Tính diện tích xung quanh
S
x
q
của
(
N
)
.
Đọc tiếp
Cho tứ diện đều A B C D có cạnh bằng 3 a . Hình nón ( N ) có đỉnh A và đường tròn đáy là đường tròn ngoại tiếp tam giác B C D . Tính diện tích xung quanh S x q của ( N ) .
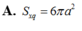
![]()
![]()

Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và chiều cao bằng 2a. Diện tích xung quanh của hình nón đỉnh S với đáy là hình tròn nội tiếp ABCD là
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và chiều cao bằng 2a. Diện tích xung quanh của hình nón đỉnh S với đáy là hình tròn nội tiếp ABCD là
![]()
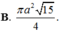
![]()
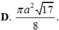
Cho tứ diện đều ABCD có cạnh bằng 3a. Hình nón (N) có đỉnh A và đường tròn đáy là đường ngoại tiếp tam giác BCD. This diện tích xung quanh
S
x
q
của N
Đọc tiếp
Cho tứ diện đều ABCD có cạnh bằng 3a. Hình nón (N) có đỉnh A và đường tròn đáy là đường ngoại tiếp tam giác BCD. This diện tích xung quanh S x q của N
![]()
![]()
![]()
![]()
Cho lăng trụ tam giác đều ABC.A’B’C’ có cạnh đáy bằng a và có đường cao h. Một hình trụ có các đường tròn đáy tiếp xúc với các cạnh của tam giác đáy được gọi là hình trụ nội tiếp trong lăng trụ. Hãy tính diện tích xung quanh của hình trụ nội tiếp đó.