Chọn D.
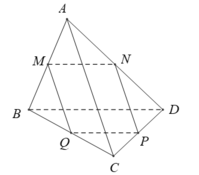
- Vì MN, PQ lần lượt là đường trung bình tam giác ABD, BCD nên:
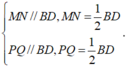
- Nên MN // PQ, MN = PQ.
⇒ tứ giác MNPQ là hình bình hành.
- Do đó MP và NQ cùng thuộc mặt phẳng MNPQ và hai đường thẳng này cắt nhau.
Chọn D.

- Vì MN, PQ lần lượt là đường trung bình tam giác ABD, BCD nên:
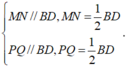
- Nên MN // PQ, MN = PQ.
⇒ tứ giác MNPQ là hình bình hành.
- Do đó MP và NQ cùng thuộc mặt phẳng MNPQ và hai đường thẳng này cắt nhau.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P, Q lần lượt là các điểm nằm trên các cạnh BC, SC, SD, AD sao cho MN//BS, NP//CD, MQ // CD. Những khẳng định nào sau đây là đúng?
1) PQ // SA
(2) PQ // MN
(3) tứ giác MNPQ là hình thang
(4) tứ giác MNPQ là hình bình hành
A. (4)
B. (1) và (3)
C. (2) và (3)
D. (2) và (4)
Cho tứ diện ABCD. Gọi M, N, P, Q, R và S lần lượt trung điểm của AB, CD, BC, AD, AC và BD. Chứng minh rằng tứ giác MNPQ là hình bình hành. Từ đó suy ra ba đoạn thẳng MN, PQ và RS cắt nhau tại trung điểm mỗi đoạn.
Cho tứ diện ABCD. Gọi M và N lần lượt là trung điểm của AB và CD. Mặt phẳng α qua MN cắt AD; BC lần lượt tại P và Q. Biết MP cắt NQ tại I. Ba điểm nào sau đây thẳng hàng?
A. I; A; C
B. I; B; D
C. I; A: B
D. I; C; D
Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các đoạn AC, BD, AD và có MN = PQ . Chứng minh rằng AB ⊥ CD.
Chỉ cần đáp án thôi ạ
Cho tứ diện ABCD. Các điểm M,N,P lần lượt là trung điểm của các cạnh AB,AC,CD mệnh đề sai là
A. MN // (ACD)
B. BC //(DMN)
C. NP //(ABD)
D. AD //(MNP)
Cho tứ diện ABCD. Trên các cạnh AD và BC lần lượt lấy M, N sao cho AM = 3MD; BN = 3NC. Gọi P, Q lần lượt là trung điểm của AD và BC. Chứng minh các vectơ M N → , D C → , P Q → đồng phẳng.
Cho hình bình hành ABCD, ABCD không là hình thoi. Trên đường chéo BD lấy 2 điểm M, N sao cho BM= MN = ND, Gọi P, Q là giao điểm của AN và CD; CM và AB. Tìm mệnh đề sai
A. P và Q đối xứng qua O
B. M và N đối xứng qua O
C. M là trọng tâm tam giác ABC
D. M là tâm đường tròn ngoại tiếp tam giác ABC
Cho tứ diện ABCD. Gọi M; N; P lần lượt là các điểm thuộc cạnh AB; AC; BD; M N ∩ B C = I ; M P ∩ A D = J ; N J ∩ I P = K . Tìm mệnh đề đúng:
A. C; D; I thẳng hàng
B. C; M; K thẳng hàng
C. C; D; K thẳng hàng
D. M; I; J thẳng hàng
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. M là một điểm di động trên đoạn AB. Một mặt phẳng (α) đi qua M và song song với SA và BC; (α) cắt SB, SC và CD lần lượt tại N, P và Q
a) Tứ giác MNPQ là hình gì?
b) Gọi I là giao điểm của MN và PQ. Chứng minh rằng I nằm trên một đường thẳng cố định.