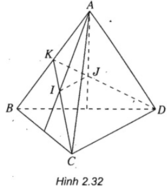
Gọi K là trung điểm của AB.
Vì I là trọng tâm của tam giác ABC nên I ∈ KC và vì J là trọng tâm của tam giác ABD nên J ∈ KD.
Từ đó suy ra
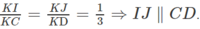

Gọi K là trung điểm của AB.
Vì I là trọng tâm của tam giác ABC nên I ∈ KC và vì J là trọng tâm của tam giác ABD nên J ∈ KD.
Từ đó suy ra
Cho tứ diện ABCD. Gọi G 1 và G 2 lần lượt là trọng tâm của tam giác ACD và BCD. Chứng minh rằng G 1 G 2 song song với các mặt phẳng (ABC) và (ABD).
Cho tứ diện ABCD. Gọi I, J lần lượt là trọng tâm các tam giác ABC và ABD. Trong các mệnh đề sau, mệnh đề nào đúng?
A. IJ//AB
B. IJ // DC
C. IJ//BD
D. IJ//AC
Cho tứ diện ABCD. Gọi G 1 , G 2 , G 3 lần lượt là trọng tâm các tam giác ABC, ACD, ABD. Chứng minh rằng ( G 1 G 2 G 3 ) / / ( B C D ) .
1. Cho hình chóp S.ABCD có ABCD là hình bình hành . Tìm giáo tuyến của 2 mặt phẳng sau:
a) (SAB) với (SCD)
b) ( SBC) và (SAD)
2. Cho tứ diện ABCD có I , J lần lượt là trọng tâm ∆ ABC và ∆ ACD . Chứng minh IJ // BD
Cho tứ diện ABCD. Gọi M,N,P lần lượt là trung điểm của các cạnh BC, BD,CD.
a. Xác định giao tuyến của hai mặt phẳng (AMN) và (ACD).
b. Chứng minh rằng đường thẳng BC song song với mặt phẳng (ANP)
c. Gọi G, H lần lượt là trọng tâm của tam giác ABC và ACD. Chứng minh GH // BD.
Cho tứ diện ABCD. M, N lần lượt là trọng tâm của các tam giác ABC, ABD. Thiết diện của tứ diện với mặt phẳng (∝) chứa MN và song song với AB là hình gì?
A. tam giác
B. hình bình hành
C. hình thoi
D. hình thang có đúng một cặp cạnh song song
Cho tứ diện ABCD có thể tích V . Gọi M, N, P, Q lần lượt là trọng tâm tam giác ABC, ACD, ABD và BCD . Thể tích khối tứ diện MNPQ bằng
A. 4 V 9
B. V 27
C. V 9
D. 4 V 27
Cho tứ diện ABCD có hai mặt ABC và ABD là các tam giác đều chứng minh rằng AB vuông góc với CD
Cho tứ diện ABCD. Gọi G và E lần lượt là trọng tâm của tam giác ABD và ABC. Mệnh đề nào dưới đây đúng:
A. GE//CD
B. GE và CD chéo nhau
C. GE cắt AD
D. GE cắt CD