Phương pháp:
Cho tứ diện ABCD có AB, AC, AD đôi một vuông góc, khi đó ![]()
Cách giải:
![]()
Chọn: A
Phương pháp:
Cho tứ diện ABCD có AB, AC, AD đôi một vuông góc, khi đó ![]()
Cách giải:
![]()
Chọn: A
Cho tứ diện ABCD có AB,AC,AD đôi một góc vuông, AB =4cm, A C = 5 c m , AD= 3cm. Thể tích khối tứ diện ABCD bằng
![]()
![]()
![]()
![]()
Cho tứ diện ABCD có các cạnh AB,AC, AD vuông góc với nhau từng đôi một và AB=3a, AC=6a, AD=4a. Gọi M, N, P lần lượt là trung điểm các cạnh BC, CD, BD. Tính thể tích khối đa diện AMNP.
![]()
![]()
Cho tứ diện ABCD có các cạnh AB, AC, AD vuông góc với nhau từng đôi một và AB = 3cm, AC = 6cm, AD = 4cm. Gọi M, N, P lần lượt là trung điểm các cạnh BC, CD, DB. Tính thể tích khối đa diện AMNP.
A. 3 a 3
B. 12 a 3
C. a 3
D. 2 a 3
Cho tứ diện ABCD có các cạnh AB, AC và AD đôi một vuông góc với nhau, AB = 6a, AC = 5a, AD = 4a. Gọi M, N, P tương ứng là trung điểm của các cạnh BC, CD, DB. Thể tích V của tứ diện AMNP là:
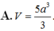
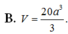
![]()
![]()
Cho tứ diện ABCD có AB=CD=3, AD=BC=5, AC=BD=6. Tính thể tích khối cầu ngoại tiếp tứ diện ABCD.
![]()
![]()
![]()
![]()
Cho tam giác ABC vuông tại A có AB < AC, đường cao AH. Kẻ HD vuông góc với AB tại D, HE vuông góc với AC tại E. a) Tứ giác ADHE là hình gì? Vì sao? b) Tính diện tích của tứ giác ADHE nếu AD = 4 cm; AH = 5 cm. c) Lấy hai điểm I và K sao cho D là trung điểm của BI và D cũng là trung điểm của HK. Chứng minh tứ giác BKIH là hình bình hành; AK vuông góc với IH.
Cho tứ diện ABCD có AB = 3, AC = 2, AD = 6, BAC = 900, CAD = 1200, BAD = 600 . Thể tích khối tứ diện ABCD bằng
A. 6 2
B. 2 2 3
C. 2
D. 3 2
Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (ABC). Biết rằng AC = AD = 4cm, AB = 3cm, BC = 5cm. Tính thể tích tứ diện ABCD
Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (ABC), AC = AD = 4, AB = 3, BC = 5. Tính khoảng cách từ điểm A đến mặt phẳng (BCD).
A. 34 12
B. 12 34
C. 769 60
D. 60 769