Chọn A
Cách 1.
Giả sử ![]() Đặt
Đặt ![]() Khi đó
C
1
,
C
2
, C là ba tập con không giao nhau của S và S =
C
1
∪
C
2
∪
C
Khi đó
C
1
,
C
2
, C là ba tập con không giao nhau của S và S =
C
1
∪
C
2
∪
C
Khi đó mỗi phần tử x ∈ S có 3 khả năng: Hoặc thuộc tập C 1 hoặc thuộc tập C 2 hoặc thuộc tập C.
Do đó 12 phần tử sẽ có 3 12 cách chọn.
Trong các cách chọn nói trên có 1 trường hợp C 1 = C 2 = ∅ , C = S
Các trường hợp còn lại thì lặp lại 2 lần (đổi vai trò C 1 và C 2 cho nhau).
Do đó số cách chia là 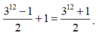
Cách 2.
Đặt S = S 1 ∪ S 2
Nếu
S
1
có k phần tử ![]()
![]()
![]()
![]()
Vậy số cách chọn 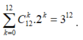
Nhưng trường hợp ![]() giống nhau và không hoán vị nên có
giống nhau và không hoán vị nên có  cách
cách





