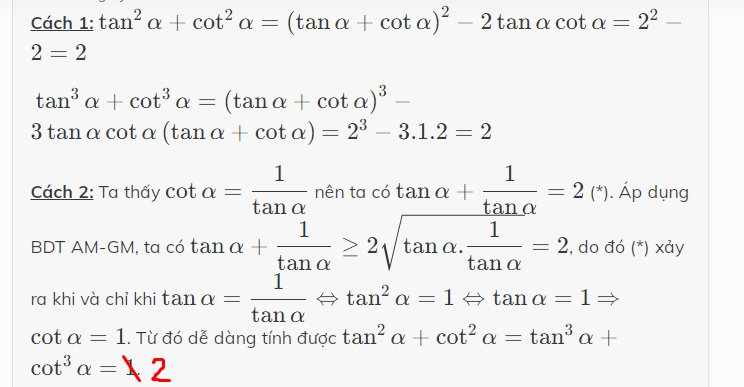Cách 1: \(\tan^2\alpha+\cot^2\alpha=\left(\tan\alpha+\cot\alpha\right)^2-2\tan\alpha\cot\alpha\) \(=2^2-2=2\)
\(\tan^3\alpha+\cot^3\alpha=\left(\tan\alpha+\cot\alpha\right)^3-3\tan\alpha\cot\alpha\left(\tan\alpha+\cot\alpha\right)\) \(=2^3-3.1.2=2\)
Cách 2: Ta thấy \(\cot\alpha=\dfrac{1}{\tan\alpha}\) nên ta có \(\tan\alpha+\dfrac{1}{\tan\alpha}=2\) (*). Áp dụng BDT AM-GM, ta có \(\tan\alpha+\dfrac{1}{\tan\alpha}\ge2\sqrt{\tan\alpha.\dfrac{1}{\tan\alpha}}=2\), do đó (*) xảy ra khi và chỉ khi \(\tan\alpha=\dfrac{1}{\tan\alpha}\Leftrightarrow\tan^2\alpha=1\Leftrightarrow\tan\alpha=1\) \(\Rightarrow\cot\alpha=1\). Từ đó dễ dàng tính được \(\tan^2\alpha+\cot^2\alpha=\tan^3\alpha+\cot^3\alpha=2\).
(Tuyệt đối không được dùng cách 2 khi \(\tan\alpha\) hoặc \(\cot\alpha\) âm nhé, vì bất đẳng thức AM-GM chỉ dùng cho số dương thôi.)
Chỗ này phải sửa thành 2 mới đúng nhé.
tuỳ ý giá trị biểu thức