2). Gọi PQ giao BC tại D, AQ giao BR tại E ta có các biến đổi góc sau
E Q D ^ = D Q B ^ − A Q B ^ = P R B ^ − A C B ^ = R B C ^ = E B D ^ .
Vậy tứ giác BEDQ nội tiếp, suy ra B E Q ^ = B D Q ^ = 90 0 ⇒ B R ⊥ A Q

2). Gọi PQ giao BC tại D, AQ giao BR tại E ta có các biến đổi góc sau
E Q D ^ = D Q B ^ − A Q B ^ = P R B ^ − A C B ^ = R B C ^ = E B D ^ .
Vậy tứ giác BEDQ nội tiếp, suy ra B E Q ^ = B D Q ^ = 90 0 ⇒ B R ⊥ A Q
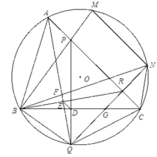
Cho tam giác nhọn ABC nội tiếp đường tròn (O). M, N là hai điểm thuộc cung nhỏ A C ⏜
sao cho MN song song với AC và tia BM nằm giữa hai tia BA, BN. BM giao AC tại P.
Gọi Q là một điểm thuộc cung nhỏ B C ⏜ sao cho PQ vuông góc với BC. QN giao AC tại R
3) Gọi F là giao của AQ và BN. Chứng minh rằng A F B ^ = B P Q ^ + A B R ^ .
Bài 4: (3,5 điểm) Cho đường tròn tâm (O) với dây AB cố định không phải đường kính. Gọi C là điểm thuộc cung lớn AB sao cho tam giác ABC nhọn. M; N lần lượt là điểm chính giữa của cung nhỏ AB; AC. Gọi I là giao điểm của BN và CM. Dây MN cắt AB và AC lần lượt tại H và K.
a) Chứng minh tứ giác BMHI nội tiếp
b) Chứng minh MK.MN = MI.MC
c) Chứng minh tứ giác AKI cân tại K và tứ giác AHIK là hình thoi.
Cho tam giác nhọn ABC nội tiếp đường tròn tâm O.
Gọi M là một điểm trên cung nhỏ B C ⏜ (M khác B; C và AM không đi qua O).
Giả sử P là một điểm thuộc đoạn thẳng AM sao cho đường tròn đường kính MP cắt cung nhỏ BC tại điểm N khác M.
1). Gọi D là điểm đối xứng với điểm M qua O. Chứng minh rằng ba điểm N, P, D thẳng hàng.
2). Đường tròn đường kính MP cắt MD tại điểm Q khác M. Chứng minh rằng P là tâm đường tròn nội tiếp tam giác AQN.
Cho tam giác ABC vuông tại A nội tiếp đường tròn (O) và ngoại tiếp đường tròn (I). Gọi M,N lần lượt là tiếp điểm của (I) với AC,AB. Đường trung bình song song với BC của tam giác ABC cắt (O) tại hai điểm P,Q. Chứng minh rằng M,N,P,Q cùng nằm trên một đường tròn.
Cho tam giác nhọn ABC nội tiếp đường tròn tâm O.
Gọi M là một điểm trên cung nhỏ B C ⏜ (M khác B; C và AM không đi qua O).
Giả sử P là một điểm thuộc đoạn thẳng AM sao cho đường tròn đường kính MP cắt cung nhỏ BC tại điểm N khác M.
2). Đường tròn đường kính MP cắt MD tại điểm Q khác M. Chứng minh rằng P là tâm đường tròn nội tiếp tam giác AQN.
Cho tam giác nhọn ABC, đường cao AH, H thuộc BC. P thuộc AB sao cho CP là phân giác góc BCA.
Giao điểm của CB và AH là Q. Trung trực của PQ cắt AH và BC lần lượt tại E, F.
1). PE giao AC tại K. Chứng minh rằng PK vuông góc AC.
Cho tam giác ABC nhọn(AB<AC) nội tiếp đường tròn nội tiếp đường tròn
tâm O
ĐỀ SỐ 2
Kẻ đường cao AH. Gọi M, N là hình chiếu vuông góc của H lên AB, AC. Kẻ NE
vuông góc với AH. Đường thẳng vuông góc với AC kẻ từ C cắt đường tròn tại I và
cắt tia AH tại D. Tia AH cắt đường tròn tại F
a) Chứng minh ABC+ACB=AIC và tứ giác DENC nội tiếp.
b) Chứng minh AM. AB = AN . AC.
c) Chứng minh tứ giác BFIC là hình thang cân.
d) Chứng minh tứ giác BMED nội tiếp .
Cho đường tròn tâm O , đường kính AB . Trên tiếp tuyến của đường tròn ( O ) tại A lấy điểm M (M khác A ) . Từ M vẽ tiếp tuyến thứ hai MC với ( O ) ( C là tiếp điểm ) . Kẻ CH vuông góc với AB (H thuộc AB ). Tia MB cắt đường tròn ( O ) tại K và cắt CH tại N . Gọi I là giao điểm của OM và AC
a) Chứng minh Tứ giác AKNH nội tiếp
b ) Chứng minh BHAM = OA . HC .
c ) Chứng minh IN song song với AB .
Cảm ơn các bạn nhé!! Mình cần gấp
Cho tam giác nhọn ABC (AB<AC). Đường tròn (O) đường kính BC cắt AB và AC lần lượt tại E và D. Gọi H là giao điểm của BD và CE. Tia AH cắt BC tại F,
a) Chứng minh AF vuông góc với BC và tứ giác BEHF nội tiếp
b) Gọi M là trung điểm của CH. Chứng minh tứ giác OMEF nội tiếp
c) DF cắt Ce tại N. Qua N kẻ đường thẳng vuông góc với CE cắt BC và BD lần lượt tại I và K. Chứng minh N là trung điểm của IK