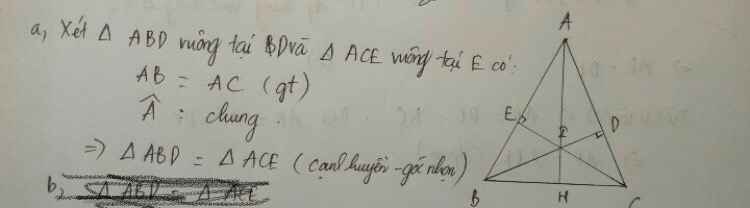Các câu hỏi tương tự
Cho 4ABC nhọn có AB = AC. Kẻ BD ? AC tại D, kẻ CE ? AB tại E. Gọi I là giao điểm của BD và CE. Chứng minh rằng:
a) 4ABD = 4ACE
b) EI = DI
c) AI ? BC
( số 4 là kí hiệu tam giác, dấu hỏi chấm là kí hiệu vuông góc)
bạn nào giúp mình với
Cho tam giác nhọn ABC có AB=AC.Kẻ BD vuông góc AC tại D,kẻ CE vuông góc AB tại E.Gọi I là giao điểm của BD và CE.CMR:
A)Tam giác ABD=Tam giác ACE
B)EI=DI
C)AI vuông góc BC
Cho tam giác nhọn ABC , kẻ BD vuông góc với AC tại D , CE vuông góc với AB tại E . Gọi I là giao điểm của BD và CE . Chứng minh rằng:
a; tam giác ABD = tam giác ACE
b ;EI=DI
c; AI vuông góc với BC
Cho tam giác ABC cân tại A(A<90độ),kẻ CE⊥AB(E thuộc AB),BD⊥AC(d thuộc AC).
a) chứng minh BE=CD
b) Gọi I là giao điểm của BD và CE.chứng minh AI là tia phân giác của góc BAC.
c) Gọi M là trung điểm của BC, chứng minh ba điểm A,I,M thảng hàng.
bài 4: cho tam giác ABC cân tại A (góc A nhỏ hơn 90 độ). Kẻ BD vuông góc với AC tại D và CE vuông góc AB tại E .
a, chúng minh tam giác ABD= tam giác ACE, từ đó suy ra góc ABD= góc ACE
b, gọi H là giao điểm của BD và CE , chứng minh tam giác BHC là tam giác cân so sánh HB và HD
Bài 5: Cho tam giác ABC có ABAC, Kẻ BDperpAC tại D, Kẻ CEperpAB tại E, BD cắt CE tại Ha) Chứng minh: DeltaABD DeltaACEb) Chứng minh: DeltaBCD DeltaCBEc) Chứng minh: DeltaBCD DeltaCHDd) Chứng minh: AH là tia phân giác của góc BAC
Đọc tiếp
Bài 5: Cho tam giác ABC có AB=AC, Kẻ BD\(\perp\)AC tại D, Kẻ CE\(\perp\)AB tại E, BD cắt CE tại H
a) Chứng minh: \(\Delta\)ABD = \(\Delta\)ACE
b) Chứng minh: \(\Delta\)BCD = \(\Delta\)CBE
c) Chứng minh: \(\Delta\)BCD = \(\Delta\)CHD
d) Chứng minh: AH là tia phân giác của góc BAC
cho tam giác ABC có B và C là góc nhọn. Qua B kẻ đoạn thẳng BD vuông góc với AC ( D thuộc AC ). Qua C kẻ đường thẳng CE vuông góc với AB ( E thuộc AB ). Gọi H là giao điểm BD và CE. Hãy tìm mối liên hệ giữa:
a, ABD và ACE
b, A và DHE
Cho tam giác ABC có AB bằng ac kẻ BD vuông góc với AC tại D kẻ CE vuông góc với AB tại E Gọi I là giao điểm của BD và CE a) tam giác abd = tam giác ace b) tam giác BEI = tam giácCDI
Cho tam giác ABC cân tại A (A< 90 độ) Kẻ BD vuông góc với AC tại D , kẻ CE Vuông góc với AB tại E:
a,Chứng minh Δ ABD cân
b,Chứng minh DE song song với BC
c,Gọi I là giao điểm của BD và CE . Chứng minh IB=IC
d,Chứng minh AI vuong góc với BC