Các câu hỏi tương tự
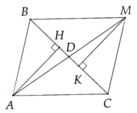
Cho tam giác nhọn ABC (AB < AC). Gọi D là trung điểm của BC. Trên tia đối của tia DA lấy điểm M sao cho DM = DA.
a) Chứng minh AC = BM và AC // BM.
b) Chứng minh ΔABM =ΔMCA.∆ABM =∆MCA.
c) Kẻ AH ⊥BC, MK⊥ BC (H, K ∈ BC)AH ⊥BC, MK⊥ BC (H, K ∈ BC). Chứng minh BK = CH.
d) Chứng minh HM // AK.
1. Cho ∆ABC vuông tại A (AB AC). Vẽ tia BD là phân giác của góc ABC (D ∈ AC). Trên cạnh BC lấy điểm E sao cho BA BE.a. Chứng minh: ∆BAD ∆BEDb. Từ A kẻ AH ⊥ BC tại H. Chứng minh: AH // DEc. Trên tia đối của tia ED lấy điểm K sao cho ED EK. Chứng minh: Góc EKC góc ABC2.Cho tam giác ABC vuông tại A. Trên cạnh BC lấy điểm E sao cho BE BA. Phân giác góc B cắt AC tại D. a. Chứng minh ∆ABD Đồng ý∆EBD và DE ⊥ BCb. Gọi K là giao điểm của tia ED và tia BA. Chứng minh AK EC.c. Gọi M là trung điểm c...
Đọc tiếp
1. Cho ∆ABC vuông tại A (AB < AC). Vẽ tia BD là phân giác của góc ABC (D ∈ AC). Trên cạnh BC lấy điểm E sao cho BA = BE.
a. Chứng minh: ∆BAD = ∆BED
b. Từ A kẻ AH ⊥ BC tại H. Chứng minh: AH // DE
c. Trên tia đối của tia ED lấy điểm K sao cho ED = EK. Chứng minh: Góc EKC = góc ABC
2.
Cho tam giác ABC vuông tại A. Trên cạnh BC lấy điểm E sao cho BE = BA. Phân giác góc B cắt AC tại D.
a. Chứng minh ∆ABD = Đồng ý∆EBD và DE ⊥ BC
b. Gọi K là giao điểm của tia ED và tia BA. Chứng minh AK = EC.
c. Gọi M là trung điểm của KC. Chứng minh ba điểm B, D, M thẳng hàng.
3.
Cho tam giác ABC vuông tại A (AB < AC). Trên cạnh BC lấy điểm M sao cho BA = BM. Gọi E là trung điểm AM.
a.Chứng minh: ∆ABE = ∆MBE.
b. Gọi K là giao điểm BE và AC. Chứng minh: KM ⊥ BC,
c. Qua M vẽ đường thẳng song song với AC cắt BK tại F. Trên đoạn thẳng KC lấy điểm Q sao cho KQ = MF. Chứng minh: góc ABK = QMC
4
Cho tam giác ABC có AB = AC, lấy M là trung điểm của BC.
a) Chứng minh ∆ABM = ∆ACM
b) Kẻ ME ⊥ AB tại Em kẻ MF ⊥ AC tại F. Chứng minh AE = AF.
c) Gọi K là trung điểm của EF. Chứng minh ba điểm A, K, M thẳng hàng
d) Từ C kẻ đương thẳng song song với AM cắt tia BA tại D. Chứng minh A là trung điểm của BD.
Cho tam giác ABC có AB = AC và AC > BC .
Gọi H là trung điểm của BC.
a) Chứng minh : .
b) Trên tia đối của HA lấy điểm M sao cho HA =
HM . C/m: AB // MC
c) Từ B vẽ a ⊥ AC tại K, trên tia đối của KC lấy
điểm D sao cho KD = KC. C/m : BK là phân
giác của góc DBC
d) Trên tia đối của BA lấy điểm E sao cho BE =
AD. C/m: CE = CA
Cho tam giác ABC có AB = AC và AC > BC .
Gọi H là trung điểm của BC.
a) Chứng minh : .
b) Trên tia đối của HA lấy điểm M sao cho HA =
HM . C/m: AB // MC
c) Từ B vẽ a ⊥ AC tại K, trên tia đối của KC lấy
điểm D sao cho KD = KC. C/m : BK là phân
giác của góc DBC
d) Trên tia đối của BA lấy điểm E sao cho BE =
AD. C/m: CE = CA.
Cho tam giác ABC có AB = AC và AC > BC. Gọi H là trung điểm cạnh BC.
a) Chứng minh ∆ABH = ∆ACH.
b) Trên tia đối của tia HA lấy điểm M sao cho HA = HM. Chứng minh AB//MC.
c) Từ B vẽ đường thẳng vuông góc với AC tại K, trên tia đối của tia KC lấy điểm D sao cho KD = KC.
Chứng minh tia BK là tia phân giác của góc DBC.
d) Trên tia đối của tia BA lấy điểm E sao cho BE = AD. Chứng minh CE = CA.
Cho tam giác ABC vuông tại A. Trên cạnh BC lấy điểm K sao cho BK=BA. Gọi M là trung điểm của đoạn thẳng AK. a) Chứng minh: ∆AMB=∆KMB b) Đường thẳng BM cắt đường thẳng AC tại D. Chứng minh: DK vuông góc với BC. c) Trên tia đối của tia AB lấy điểm H sao cho ah=kc chứng minhh d k thẳng hàng
Cho tam giác abc có ab=ac, góc a nhọn. Gọi M là trung điểm của bc. Kẻ bh vuông góc với ac ( h thuộc ac). Trên tia hm lấy điểm k sao cho m là trung điểm của hk. a)Chứng minh tâm giác mhb= tam giác mkc. b) Trên tia đối của tia hb lấy điêm i sao cho hi=hk.Chứng minh ic song song với hk. c) Chứng minh góc bac= 2 lần tam giác bic
Bài 1. Cho góc xOy, có Ot là tia phân giác. Lấy điểm A trên tia Ox, điểm B trên tia Oy sao cho OA OB. Vẽ đoạn thẳng AB cắt Ot tại M. Chứng minh
a) OAM OBM;
b) AM BM; OM AB
c) OM là đường trung trực của AB
d) Trên tia Ot lấy điểm N . Chứng minh NA NB
Bài 2. Cho ABC vuông tại A, trên tia đối của tia CA lấy điểm K sao cho CK CA, từ K kẻ KE vuông góc với đường thẳng AC. Chứng mỉnhằng:
a) AB // KE b) ABC KEC ; BC CE
Bài 3. Cho góc nhọn xOy. Trên tia Ox lấy hai điểm A, C....
Đọc tiếp
\(Bài 1. Cho góc xOy, có Ot là tia phân giác. Lấy điểm A trên tia Ox, điểm B trên tia Oy sao cho OA = OB. Vẽ đoạn thẳng AB cắt Ot tại M. Chứng minh a) OAM = OBM; b) AM = BM; OM AB c) OM là đường trung trực của AB d) Trên tia Ot lấy điểm N . Chứng minh NA = NB Bài 2. Cho ABC vuông tại A, trên tia đối của tia CA lấy điểm K sao cho CK = CA, từ K kẻ KE vuông góc với đường thẳng AC. Chứng mỉnhằng: a) AB // KE b) ABC = KEC ; BC = CE Bài 3. Cho góc nhọn xOy. Trên tia Ox lấy hai điểm A, C. Trên tia Oy lấy hai điểm B,D sao cho OA = OB, AC = BD. a) Chứng minh: AD = BC. b) Gọi E là giao điểm AD và BC. Chứng minh: EAC = EBD c) Chứng minh: OE là phân giác của góc xOy, OE CD Bài 4. Cho ABC coù BÂ=900, gọi M là trung điểm của BC. Trên tia đối của tia AM lấy điểm E sao cho ME = MA. a) Tính BCE b) Chứng minh BE // AC. Bài 5. Cho ABC, lấy điểm D thuộc cạnh BC ( D không trùng với B,C). Gọi Mlà trung điểm của AD. Trên tia đối của tia MB lấy điểm E sao cho ME= MB, trên tia đối của tia MC lấy điểm F sao cho MF= MC. Chứng minh rằng: a) AME = DMB; AE // BC b) Ba điểm E, A, F thẳng hàng c) BF // CE Bài 6: Cho có B = C , kẻ AH BC, H BC . Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Chứng minh: a) AB = AC b) ABD = ACE c) ACD = ABE d) AH là tia phân giác của góc DAE e) Kẻ BK AD, CI AE. Chứng minh ba đường thẳng AH, BK, CI cùng đi qua một điểm. \)
cho tam giác abc gọi m là trung điểm của bc qua c kẻ đường thẳng song song với ab cắt tia am ở d a chứng minh rằng m là trung điểm của ad b, gọi n là trung điểm của ac trên tia đối của nb lấy k sao cho ak = nb chứng minh ck=ab c, chứng minh ở điểm k,c,d thẳng hàng
vẽ hình hộ mình nhé giúp mình vs mình đnag gấp lắm ak