Các câu hỏi tương tự
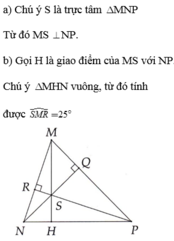
Cho \(\Delta\)MNP có 3 góc nhọn,các đường cao NQ,PR cắt nhau tại S
a)Chứng minh MS\(\perp\)NP
b)Cho góc MNP=65 độ tính góc SMR
Nhanh với ạCho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O; R). Các đường cao AD, BE, CF của tam giác ABC cắt nhau tại H.Chứng minh tứ giác BFECnội tiếpTia AO cắt đường tròn (O) tại K. Chứng minh AC AK. AD;Gọi M là trung điểm của BC. Chứng minh ba điểm H, M, K thẳng hàng.Cho BC cố định, A chuyển động trên cung lớn BC sao cho tam giác ABC có ba góc nhọn, chứng minh diện tích hình tròn ngoại tiếp tam giác AEF không đổi.
Đọc tiếp
Nhanh với ạ
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O; R). Các đường cao AD, BE, CF của tam giác ABC cắt nhau tại H.Chứng minh tứ giác BFECnội tiếpTia AO cắt đường tròn (O) tại K. Chứng minh AC = AK. AD;Gọi M là trung điểm của BC. Chứng minh ba điểm H, M, K thẳng hàng.Cho BC cố định, A chuyển động trên cung lớn BC sao cho tam giác ABC có ba góc nhọn, chứng minh diện tích hình tròn ngoại tiếp tam giác AEF không đổi.
Bài 1 : Cho tam giác ABC có 3 đường trung tuyến AD , BE , CF cắt nhau tại G . Chứng minh rằng a, frac {AB+AC}{2}b,BE+CF frac{3}{2}BCc, frac{3}{4}(AB+BC+AC)AD+BE+CFAB+BC+ACBài 2 : Cho tam giác ABC , tia phân giác góc B , C cắt nhau tại O . Từ A vẽ một đường thẳng vuông góc với OA , cắt OB , OC tại M,N . Chứng minh : BM vuông góc với BN . CM vuông góc với CNBài 3 . Cho tam giác ABC , góc B 450 , đường cao AH , phân giác BD của tam giác ABC , biết góc BDA 450 . Chứng minh HD//AB Bài 4 . Cho tam...
Đọc tiếp
Bài 1 : Cho tam giác ABC có 3 đường trung tuyến AD , BE , CF cắt nhau tại G . Chứng minh rằng
\(a, \frac {AB+AC}{2}\)
\(b,BE+CF < \frac{3}{2}BC\)
\(c, \frac{3}{4}(AB+BC+AC)<AD+BE+CF<AB+BC+AC\)
Bài 2 : Cho tam giác ABC , tia phân giác góc B , C cắt nhau tại O . Từ A vẽ một đường thẳng vuông góc với OA , cắt OB , OC tại M,N . Chứng minh : BM vuông góc với BN . CM vuông góc với CN
Bài 3 . Cho tam giác ABC , góc B = 450 , đường cao AH , phân giác BD của tam giác ABC , biết góc BDA = 450 . Chứng minh HD//AB
Bài 4 . Cho tam giác ABC không vuông , các đường trung trực của AB , AC cắt nhau tại O , cắt BC theo thứ tự M,N . Chứng minh AO là phân giác của góc MAN .
Bài 5 : Cho tam giác ABC nhọn , đường cao BD , CE cắt nhau tại H . Lấy K sao cho AB là trung trực của HK . Chứng minh góc KAB = góc KCB
Cho tam giác MNP nhọn có góc M= 50 độ, đường cao NK lấy điểm E thuộc đoạn MN sao cho góc MPE = 40 độ. Kéo dài NK cắt PE ở I . Chứng minh
a) góc MNK = góc MPE
b) MI vuông góc NP
c) cho tam giác MNP cân ở M. Tính các góc của tam giác MIP
Cho tam giác MNP cân tại M , vẽ MH vuông góc với NP
a ) Chứng minh : Tam giác MHN = Tam giác MHP
b ) Chứng minh MH là phân giác của tam giác MNP
c ) Tính MH nếu MN = 10 cm , NP = 12 cm
d ) Vẽ đường thẳng vuông góc với MN tại N và đường thẳng vuông góc với MP tại P , hai đường thẳng này cắt nhau tại K . Chứng minh M , K , H thẳng hàng .
Cho tam giác ABC nhọn, AB>AC, phân giác BD và CE cắt nhau tại I.a)tính các góc của tam giác DIE nếu góc A= 60 độ,b) gọi giao điểm cña BD và CE với đường cao AH của tam giác ABC lần lượt là M và N .chứng minh: BM > MN + NC.
Cho tam giác MNP có
N
^
P
^
. Vẽ phân giác MK.a) Chứng minh
M
K
P
^
−
M
K
N
^
N
^
−
P
^
.b) Đường thẳng chứa tia phân giác góc ngoài đỉnh M của tam giác MNP, cắt đường thẳng NP tại E. Chứng minh rằng:...
Đọc tiếp
Cho tam giác MNP có N ^ > P ^ . Vẽ phân giác MK.
a) Chứng minh M K P ^ − M K N ^ = N ^ − P ^ .
b) Đường thẳng chứa tia phân giác góc ngoài đỉnh M của tam giác MNP, cắt đường thẳng NP tại E. Chứng minh rằng: M E P ^ = N ^ − P ^ 2
Cho tam giác MNP có
N
^
P
^
.Vẽ phân giác MK.a) Chứng minh
M
K
P
^
−
M
K
N
^
N
^
−
P
^
b) Đường thẳng chứa tia phân giác góc ngoài đỉnh M của tam giác MNP, cắt đường thẳng NP tại E. Chứng minh rằng:...
Đọc tiếp
Cho tam giác MNP có N ^ > P ^ .Vẽ phân giác MK.
a) Chứng minh M K P ^ − M K N ^ = N ^ − P ^
b) Đường thẳng chứa tia phân giác góc ngoài đỉnh M của tam giác MNP, cắt đường thẳng NP tại E. Chứng minh rằng: M E P ^ = N ^ − P ^ 2
Cho tam giác ABC có ba góc nhọn, các đường cao AD, BE cắt nhau tại I.a) Chứng minh
C
I
⊥
A
B
.
b) Cho
A
B
C
^
50
°
. Tính
A
I
E
^
,
D
I
E
^...
Đọc tiếp
Cho tam giác ABC có ba góc nhọn, các đường cao AD, BE cắt nhau tại I.
a) Chứng minh C I ⊥ A B .
b) Cho A B C ^ = 50 ° . Tính A I E ^ , D I E ^ .