Chọn D.
Phương án A: ![]() nên
nên ![]()
nên đẳng thức ở phương án A là đúng.
Phương án B: ![]() nên
nên ![]()
nên đẳng thức ở phương án B là đúng.
Phương án C:
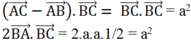
Do đó: ![]() nên phương án C là đúng.
nên phương án C là đúng.
Chọn D.
Phương án A: ![]() nên
nên ![]()
nên đẳng thức ở phương án A là đúng.
Phương án B: ![]() nên
nên ![]()
nên đẳng thức ở phương án B là đúng.
Phương án C:
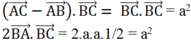
Do đó: ![]() nên phương án C là đúng.
nên phương án C là đúng.
Cho tam giác đều ABC cạnh a; với các đường cao AH; BK vẽ HI ⊥ AC. Câu nào sau đây đúng?
A. ![]()
B . ![]()
C. ![]()
D. ![]()
Cho tam giác ABC có đường cao BH ( H ở trên cạnh AC).Câu nào sau đây đúng
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Cho các mệnh đề :
A : “Nếu tam giác ABC đều có cạnh bằng a, đường cao là h thì h = a 3 2 ”
B : “Tứ giác có bốn cạnh bằng nhau là hình vuông”
C : “15 là số nguyên tố”
D : “ 225 là một số nguyên”
Chọn câu sai:
A. Mệnh đề A => B sai
B. Mệnh đề A ⇔ D đúng
C. Mệnh đề B ⇔ C đúng
D. Mệnh đề => D sai
cho tam giác ABC vuông tại A (AC>AB) Đường cao AH (H thuộc BC) trên tia HC lấy điểm D sao cho HD=HA . Đường vuông góc với BC tại D cắt AC tại E .
a) CMR hai tam giác BEC và ADC đồng dạng .Tính độ dài BE theo m=AB
b) ọi M là tung điểm của đoạn BE . CMR ha tam giác BHM và BEC đồng dạng . Tính số đo góc AHM
c) Tia AM cắt BC tại G cm \(\dfrac{\text{GB}}{\text{BC}}=\dfrac{\text{HD}}{\text{AH+HC}}\)
Câu 1 cho tam giác abc biết a=6, b=4, c=8 độ dài đường cao từ đỉnh A là 3? Diện tích tam giác là?
Câu 2 cho tam giác biết a=4, b=5, góc C= 60. Diện tích tam giác là ?
Câu 3 cho tam giác abc có a2+b2-c2 >0. Khi đó góc C là ?
E mong các ac giúp e bài toán trên nha. E cảm ơn rất nhiều ^^
Cho tam giác đều ABC với đường cao AH. Đẳng thức nào sau đây đúng?
A. H C → = H B →
B. A C → = 2 H C →
C. A H → = 3 2 H C →
D. A B → = A C →
Cho tam giác ABC có ba góc nhọn, AB < AC, nội tiếp đường tròn ( O, R). Vẽ đường kính AD của đường tròn ( O ), đường cao AH của tam giác ABC ( H thuộc BC ) và BE vuông góc với AD ( E thuộc AD ).
a) Chứng minh tứ giác AEHB nội tiếp
b) Chứng minh AH.DC = AC.BH
c) Gọi I là trung điểm của BC. Chứng minh rằng IH = IE
Cho tam giác ABC cân tại A. Gọi AE là đường cao và F là hình chiếu của E lên cạnh AC, và D là trung điểm EF . Chứng minh AD vuông góc với EF.
Câu 1. Cho tam giác ABC với A(1; 2), B(−2; 5) và C(0; 1). Gọi H, K lần lượt là chân đường cao kẻ từ
các đỉnh A, B. Hãy chỉ ra một véc-tơ pháp tuyến của mỗi đường thằng AH, BK.
Câu 2. Cho hai đường thẳng d1 : −3x + y − 2 = 0 và d2 : 2x − 3 = 0.
a) Hãy chỉ ra một VTPT của d1, d2.
b) Trong các điểm A(2; 0), B(−1; −1), C(\(\frac{3}{2}\); 1), D(\(\frac{3}{2}\); \(\frac{13}{2}\)) điểm nào thuộc d1, điểm nào thuộc d2?
Câu 3. Viết phương trình tổng quát của đường thẳng d biết
a) d đi qua điểm A(−2; 5) và có VTPT −→n = (−1; 2).
b) d đi qua điểm A(−5; 2) và vuông góc với đường thẳng BC biết tọa độ điểm B(1; 1) và
C(2; 3).
c) d đi qua điểm A(−1; 1) và song song với đường thẳng d': −4x − y + 2 = 0.