Question

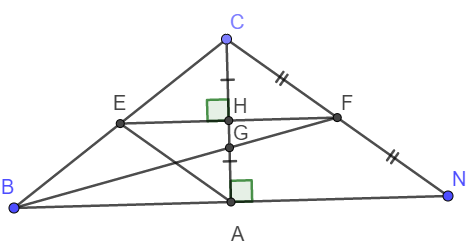
Cho tam giác CBN cân tại C có CA là đường cao, CA=15cm, BC=25cm                         

a)Tính AB và so sánh các góc trong tam giác ABC.

b)Gọi H là trung điểm AC, tại H vẽ đường vuông góc với AC, cắt BC tại E. C/m tam giác EHA=tam giác EHC và tam giác ABE cân tại A.

C)Gọi F là trung điểm NC, BF cắt AC tại G. C/m G là trọng tâm tam giác BCN và tính AG.

d)C/m E,H,F thẳng hàng.

Ai làm trước mih tck cho :))

 

Answer 1

a) Áp dụng định lý Pitago trong tam giác vuông ABC, ta có: 

 BC² = AC² + AB²

25² = 15² + AB² \(\Rightarrow ab=20\left(cm\right)\)

Xét tam giác ABC có:

  AC < AB < BC nên \(\widehat{CBA}< \widehat{BCA}< \widehat{BAC}.\)

b)  Xét tam giác vuông EHA và tam giác vuông EHC có:

Cạnh EH chung

HC = HA

\(\Rightarrow\Delta EHC=\Delta EHA\)  (Hai cạnh góc vuông)

Do \(\Delta EHC=\Delta EHA\Rightarrow\widehat{ECA}=\widehat{EAC}\)

\(\Rightarrow\widehat{EBA}=\widehat{EAB}\)    (Cùng phụ với hai góc bên trên)

Vậy nên tam giác EAB cân tại E.

c) Tam giác CBN cân tại C có CA là đường cao nên CA đồng thời là trung tuyến. 

Xét tam giác CBN có CA và BF là các đường trung tuyến mà CA giao BF tại G nên G là trọng tâm tam giác.

Theo tính chất trọng tâm ta có:

\(\frac{AG}{AC}=\frac{1}{3}\Rightarrow AG=\frac{1}{5}.15=5\left(cm\right)\)

d) Xét tam giác CBN cân tại C có CA là đường cao nên đồng thời là phân giác.

Gọi giao điểm của EH với CN là F'. Khi đó ta có \(\Delta ECH=\Delta F'CH\)   (Cạnh góc vuông và góc nhọn kề)

\(\Rightarrow CE=CF'\)

Lại có \(CE=\frac{1}{2}BC=\frac{1}{2}CN\Rightarrow CF'=\frac{1}{2}CN\)

Suy ra F' là trung điểm CN hay F' trùng F.

Vậy nên E, H, FA thẳng hàng.

Answer 2

Bài giải : 

a) Áp dụng định lý Pitago trong tam giác vuông ABC, ta có: 

 BC² = AC² + AB²

25² = 15² + AB² ⇒ab=20(cm)

Xét tam giác ABC có:

  AC < AB < BC nên ^CBA<^BCA<^BAC.

b)  Xét tam giác vuông EHA và tam giác vuông EHC có:

Cạnh EH chung

HC = HA

⇒ΔEHC=ΔEHA  (Hai cạnh góc vuông)

Do ΔEHC=ΔEHA⇒^ECA=^EAC

⇒^EBA=^EAB    (Cùng phụ với hai góc bên trên)

Vậy nên tam giác EAB cân tại E.

c) Tam giác CBN cân tại C có CA là đường cao nên CA đồng thời là trung tuyến. 

Xét tam giác CBN có CA và BF là các đường trung tuyến mà CA giao BF tại G nên G là trọng tâm tam giác.

Theo tính chất trọng tâm ta có:

AGAC =13 ⇒AG=15 .15=5(cm)

d) Xét tam giác CBN cân tại C có CA là đường cao nên đồng thời là phân giác.

Gọi giao điểm của EH với CN là F'. Khi đó ta có ΔECH=ΔF'CH   (Cạnh góc vuông và góc nhọn kề)

⇒CE=CF'

Lại có CE=12 BC=12 CN⇒CF'=12 CN

Suy ra F' là trung điểm CN hay F' trùng F.

Vậy nên E, H, FA thẳng hàng.