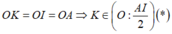Giải giùm mình vớiBài 1: Cho tam giác ABC vuông tại A và có đường cao AH 3cm. Vẽ đường tròn (A ; AH). Gọi HD là đường kính của đường tròn đó. Tiếp tuyến của đường tròn tại D cắt AC ở E.a. Chúng minh AC AE và tam giác BEC là tam giác cân.b. Tính giá trị của tích BH.ED.c. Chúng minh đường thẳng BE là tiếp tuyến của đường tròn (A ; AH).Bài 2:Cho đường tròn (O;R), dây BC khác đường kính. Hai tiếp tuyến của đường tròn (O;R) tại B và C cắt nhau tại A. Kẻ đường kính CD, kẻ BH vuông góc...
Đọc tiếp
Giải giùm mình với
Bài 1:
Cho tam giác ABC vuông tại A và có đường cao AH = 3cm. Vẽ đường tròn (A ; AH). Gọi HD là đường kính của đường tròn đó. Tiếp tuyến của đường tròn tại D cắt AC ở E.
a. Chúng minh AC = AE và tam giác BEC là tam giác cân.
b. Tính giá trị của tích BH.ED.
c. Chúng minh đường thẳng BE là tiếp tuyến của đường tròn (A ; AH).
Bài 2:
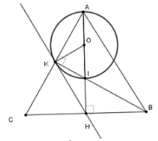
Cho đường tròn (O;R), dây BC khác đường kính. Hai tiếp tuyến của đường tròn (O;R) tại B và C cắt nhau tại A. Kẻ đường kính CD, kẻ BH vuông góc với CD tại H.
a. Chứng minh bốn điểm A, B, O, C cùng nằm trên đường tròn.
b. Chứng minh OA vuông góc với BC.
c. Chứng minh BC là phân giác góc ABH
d. Gọi E là giao điểm AC và BD. Chứng minh tam giác EAB cân