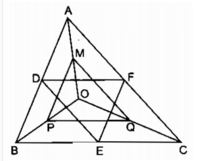
Cho tam giác ba góc nhọn ABC và một điểm O bất kì trong tam giác đó.
Ba điểm D, E, F theo thứ tự là trung điểm các cạnh AB, BC và CA. Ba điểm M, P, Q theo thứ tự là trung điểm của các đoạn thẳng OA, OB và OC.
Các tam giác DEF và MPQ có đồng dạng với nhau không ? Vì sao ? Tỉ số đồng dạng bằng bao nhiêu ?
Hãy sắp xếp các đỉnh tương ứng nếu hai tam giác đó đồng dạng.
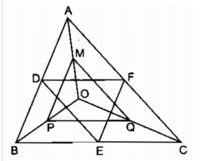
Theo giả thiết D, E, F lần lượt là trung điểm các cạnh AB, BC và CA nên DE, EF, FD là các đường trung bình của tam giác ABC. Do đó, ta có:
DE = 1/2 AC,EF = 1/2 AB,FD = 1/2 BC (1)
Mặt khác, M là trung điểm của OA, P là trung điểm của OB, Q là trung điểm của OC, xét các tam giác OAB, OBC, OCA, ta cũng có:
MP = 1/2 AB,PQ = 1/2 BC, QM = 1/2 AC. (2)
Từ đẳng thức (1) và (2), ta suy ra :
DE = QM, EF = MP, FD = PQ.
Do đó ta có: 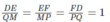
Vậy △ DEF đồng dạng △ QMP theo tỉ số đồng dạng k = 1, trong đó D, E, F lần lượt tương ứng với các đỉnh Q, M, P.