Theo định lý Pytago, tam giác ABC ( Góc A=90 độ ) có:
\(BC^2=AB^2+AC^2\)
Mà AB, BC, AC > 0 nên BC2 > AB2, BC2 > AC2 hay BC > AB và AC suy ra BC lớn nhất
Các câu hỏi tương tự
Hai tam giác ABC, A'B'C' vuông tại A và A' có AB = A'B', AC > A'C'. Không sử dụng định lý Pitago, chứng minh rằng BC > B'C'
Cho tam giác ABC trong đó BC là cạnh lớn nhất. Gọi AH là đường vuông góc kẻ từ A đến BC. So sánh AB + AC với BH + CH rồi chứng minh rằng AB + AC > BC.
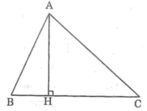
Một cách chứng minh khác của bất đẳng thức tam giác:
Cho tam giác ABC. Giả sử BC là cạnh lớn nhất. Kẻ đường vuông góc AH đến đường thẳng BC (H thuộc BC).
Dùng nhận xét về cạnh lớn nhất trong tam giác vuông ở Bài 1 để chứng minh AB + AC > BC.
Cho tam giác ABC vuông tại A.Từ A kẻ AH vuông góc với BC. Trên cạnh BC lấy đi điểmm E sao cho BE=BA. Kẻ EK vuông với AC (K thuộc AC). Chứng minh rằng: AK= AH.
(Thêm câu này nữa ạ, em bị dealine chạy sát nút rùi TvT)
CẢM ƠN MỌI NGƯỜI!
cho tam giác ABC vuông tại A . vẽ đường cao AH trên cạnh BC lấy điểm D sao cho BD=BA vẽ DK vuông góc với AC ( K thuuoccj AC )
a) chứng minh rằng tia AD là tia phân giác của HAC
b) chứng minh rằng AK = AH
c) chứng minh rằng AB+AC lớn hơn BC+AH
BÀI 1 :Chứng minh rằng trong tam giác vuông ABC ,cạnh huyền BC là cạnh lớn nhất .
bài 2 Cho tam giác ABC có ba góc nhọn ,kẻ BD vuông góc vs AC TẠI D,CE VUÔNG GÓC VS AB TẠI E.
1.CM AB>BD.
CM AC>CE
3.CM AB+AC >BD +CE
CÁC BẠN GIÚP MÌNH VS ,MÌNH ĐANG RẤT GẤP ,MÌNH SẼ LIKE LUÔN NHAAAAA
Cho tam giác ABC vuông tại A (ABAC). Trên cạnh BC lấy D sao cho DBBA. Đường vuông góc với BC tại D cắt cạnh AC tại M.a) So sánh các góc của tam giác ABC.b) Chứng minh MAMD.c) Gọi N là giao điểm của tia BA, DM. Chứng minh tam MNC là tam giác cân.d) Gọi I là trung điểm của CN. Chứng minh 3 điểm B,M,I thẳng hàng.
Đọc tiếp
Cho tam giác ABC vuông tại A (AB<AC). Trên cạnh BC lấy D sao cho DB=BA. Đường vuông góc với BC tại D cắt cạnh AC tại M.
a) So sánh các góc của tam giác ABC.
b) Chứng minh MA=MD.
c) Gọi N là giao điểm của tia BA, DM. Chứng minh tam MNC là tam giác cân.
d) Gọi I là trung điểm của CN. Chứng minh 3 điểm B,M,I thẳng hàng.
Bài 1. Cho tam giác ABC vuông tại A có góc B 53 độa) Tính góc C.b) Trên cạnh BC, lấy một điểm D sao cho BDBA. Tia phân giác của góc B cắt cạnh AC ở điểm E. Chứng minh tam giác BEA tam giác BED.Bài 2. Cho tam giác ABC có AB AC và M là trung điểm của cạnh BC.a) Chứng minh tam giác AMB tam giác AMC.b) Qua A, vẽ đường thẳng a vuông góc với AM. Chứng minh AM vuông góc với BC và a song song với BC.c) Qua C, vẽ đường thẳng b song song với AM. Gọi N là giao điểm của hai đường thẳng a và b. Chứng minh...
Đọc tiếp
Bài 1. Cho tam giác ABC vuông tại A có góc B= 53 độ
a) Tính góc C.
b) Trên cạnh BC, lấy một điểm D sao cho BD=BA. Tia phân giác của góc B cắt cạnh AC ở điểm E. Chứng minh tam giác BEA = tam giác BED.
Bài 2. Cho tam giác ABC có AB= AC và M là trung điểm của cạnh BC.
a) Chứng minh tam giác AMB = tam giác AMC.
b) Qua A, vẽ đường thẳng a vuông góc với AM. Chứng minh AM vuông góc với BC và a song song với BC.
c) Qua C, vẽ đường thẳng b song song với AM. Gọi N là giao điểm của hai đường thẳng a và b. Chứng minh tam giác AMC = tam giác CNA.
Bài 3. Cho tam giác ABC, gọi M là trung điểm của cạnh BC. Trên tia đối của tia MAlấy điểm D sao cho MD = MA.
a) Chứng minh tam giác MAB = tam giác MDC.
b) Chứng minh rằng AB = CD và AB // CD.
Bài 4. Cho tam giác ABC vuông tại A (AB < AC). Tia phân giác của góc ABC cắt AC tại D. Trên cạnh BC lấy điểm E sao cho BE = BA. Vẽ AH vuông góc với BC tại H.
a) Chứng minh rằng: tam giác ABD = tam giác EBD và AD = ED.
b) Chứng minh rằng: AH // DE.
*Vẽ hình giúp mình*
Cho tam giác ABC với độ dài 3 cạnh AB = 3cm, BC = 5cm, AC = 4cm
a) Tam giác ABC là tam giác gì? Vì sao?
b) Trên cạnh BC lấy điểm D sao cho BA = BD . Từ D vẽ Dx vuông góc với BC (Dx cắt AC tại H). Chứng minh rằng: BH là tia phân giác của góc ABC
c) Vẽ trung tuyến AM. Chứng minh tam giác ABC cân