Các câu hỏi tương tự
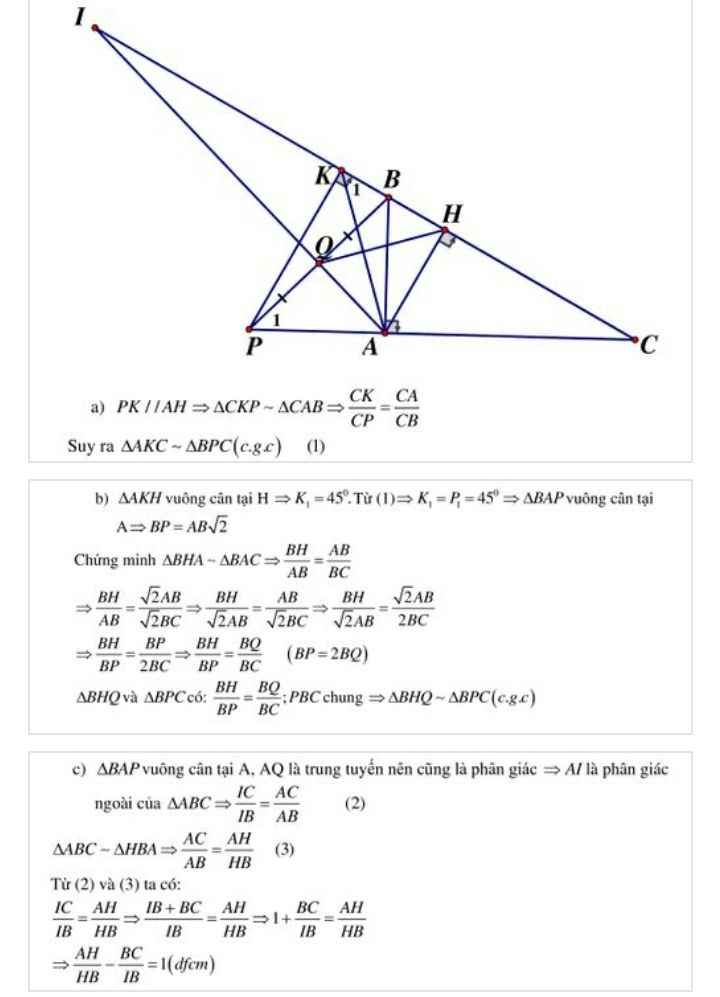
Cho tam giác ABC vuông tại A(AC>AB). Vẽ đường cao AH(H∈BC). Trên tia đối tia BC lấy K sao cho KH=HA. Qua K kẻ đường thẳng song song với AH cắt đường thẳng AC tại P. Gọi Q là trung điểm BP.
a, CMR: \(\Delta BHQ\sim\Delta BPC\)
b, AQ cắt BC tại I. CMR: \(\dfrac{AH}{HB}-\dfrac{BC}{IB}=1\)
Cho tam giác ABC vuông tại A (ACAB). Vẽ đường cao AH (�∈��)(H∈BC). Trên tia đối của tia BC lấy điểm K sao cho KHHA. Qua K kẻ đường thẳng song song với AH cắt AC tại P
a) Chứng minh: Tam giác ABC đồng dạng với tam giác KPC
b) Gọi Q là trung điểm của BP. Chứng minh: QH là đường trung trực của đoạn thẳng AK
Đọc tiếp
Cho tam giác ABC vuông tại A (AC>AB). Vẽ đường cao AH . Trên tia đối của tia BC lấy điểm K sao cho KH=HA. Qua K kẻ đường thẳng song song với AH cắt AC tại P
a) Chứng minh: Tam giác ABC đồng dạng với tam giác KPC
b) Gọi Q là trung điểm của BP. Chứng minh: QH là đường trung trực của đoạn thẳng AK
Cho tam giác ABC vuông tại A (AC > AB)đường cao AH ( H € BC ). Trên tia đối của tia bc lấy điểm K sao cho HK = HA qua K kẻ đường thẳng song song với AC cắt đường thẳng AC tại P a) Cm ∆ ABC ~ ∆ KPC b) Gọi Q là trung điểm của BP. Cm QA=QK và QH vuông góc AK c)Cm góc AKC = góc BPC d)Cm BP.HQ = BH.PC
Cho tam giác ABC vuông tại A (AC>AB). Vẽ đường cao AH \(\left(H\in BC\right)\). Trên tia đối của tia BC lấy điểm K sao cho KH=HA. Qua K kẻ đường thẳng song song với AH cắt AC tại P
a) Chứng minh: Tam giác ABC đồng dạng với tam giác KPC
b) Gọi Q là trung điểm của BP. Chứng minh: QH là đường trung trực của đoạn thẳng AK
Cho tam giác ABC vuông tại A. Vẽ đường cao AH (H\(\in\)BC). Trên tia đối của tia BC lấy điểm K sao cho KH=HA. Qua K kẻ đường thẳng song song với AH, cắt đường thẳng AC tại P.
a. Chứng minh tam giác ABC đồng dạng với tam giác KPC
b. Gọi Q là trung điểm của BP. Chứng minh: QH là đường trung trực của đoạn thẳng AK.
GIÚP MIK VỚI
Cho tam giác ABC vuông tại A (AB<AC) .Về đường cao AH. Trên ria đối của tia BC lấy điểm K sao cho KH=KA. Qua K kể đường thẳng // với AH. Cắt AC tại P
a) CM tam giác AKC đồng dạng tam giác BPC.
b) Gọi Q là trung điểm của BP . CM tam giác BHQ đồng đang tam giác BPC
c) Tia AQ cắt BC tại I. CM AH/ HB - HB / IB = 1
Cho tam giác ABC vuông tại A( AC > AB), đường cao AH( H thuộc BC). Trên tia đối của tia HB lấy điểm D sao cho HD=HA. Qua D kẻ đường thẳng vuông góc với BC cắt AC tại E.
1. Chứng minh CD.CB=CA.CE
2. tính số đo góc BEC
3. gọi M là trung điểm của đoạn BE. Tia AM cắt BC tại G.Chứng minh; GB/BC=HD/AH+HC
Cho tam giác ABC vuông tại A (ABAC), M là trung điểm của BC.Trên tia đối của tia MA lấy điểm D sao cho MDMA.a) Tứ giác ABDC là hình gì? Vì sao?b) Vẽ đường cao AH. Qua điểm D kẻ đường thẳng song song với BC, đường thẳng này cắt tia AH tại I. Chứng minh H là trung điểm của AI và BA BH.c) Chứng minh tứgiác BIDC là hình thang cân.d) Gọi K là hình chiếu vuông góc của H trên AB; P, Q lần lượt là trung điểm của AK và KH. Chứng minh IK vuông góc với BQ
Đọc tiếp
Cho tam giác ABC vuông tại A (AB<AC), M là trung điểm của BC.Trên tia đối của tia MA lấy điểm D sao cho MD=MA.
a) Tứ giác ABDC là hình gì? Vì sao?
b) Vẽ đường cao AH. Qua điểm D kẻ đường thẳng song song với BC, đường thẳng này cắt tia AH tại I. Chứng minh H là trung điểm của AI và BA = BH.
c) Chứng minh tứgiác BIDC là hình thang cân.
d) Gọi K là hình chiếu vuông góc của H trên AB; P, Q lần lượt là trung điểm của AK và KH. Chứng minh IK vuông góc với BQ
Cho tam giác ABC nhọn (abac). Kẻ đường cao AH. Gọi M là trung điểm của AB, N là điểm đối xứng với H qua M.a. C/m : Tứ giác ANBH là hình chữ nhật.b. Trên tia đối của tia HB lấy điểm E sao cho H là trung điểm của BE. Gọi F là điểm đối xứng với A qua H. C/m: ABEF là hình thoi.c. Gọi I là giao điểm của AB và NE. C/m: MI song song BC.d. Đường thẳng MI cắt AC tại K. Kẻ NQ vuông góc với KH tại Q. Chứng minh AQ vuông góc BQ.
Đọc tiếp
Cho tam giác ABC nhọn (ab<ac). Kẻ đường cao AH. Gọi M là trung điểm của AB, N là điểm đối xứng với H qua M.
a. C/m : Tứ giác ANBH là hình chữ nhật.
b. Trên tia đối của tia HB lấy điểm E sao cho H là trung điểm của BE. Gọi F là điểm đối xứng với A qua H. C/m: ABEF là hình thoi.
c. Gọi I là giao điểm của AB và NE. C/m: MI song song BC.
d. Đường thẳng MI cắt AC tại K. Kẻ NQ vuông góc với KH tại Q. Chứng minh AQ vuông góc BQ.