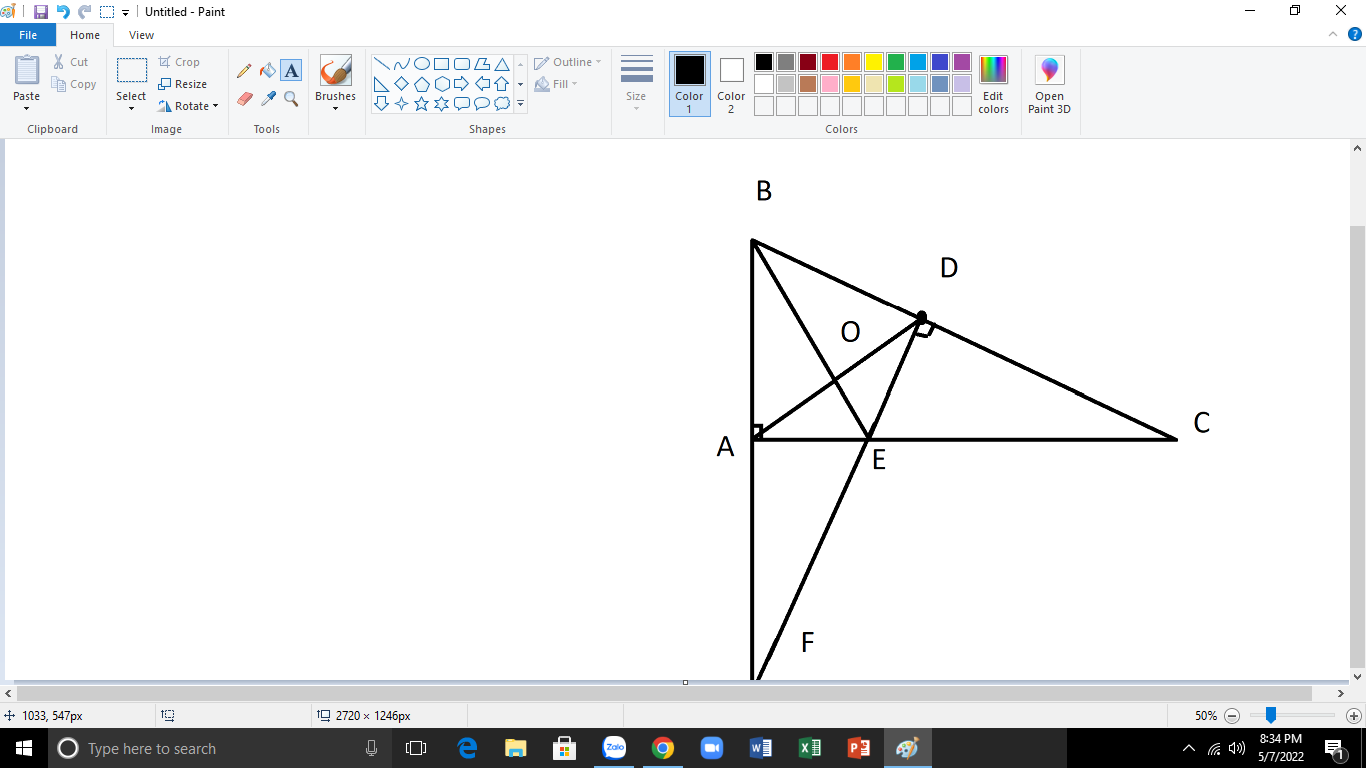
cho tam giác abc vuông tại a trên cạnh bc lấy điểm d sao cho BA = BD từ d kẻ đường thẳng vuông góc với bc cắt ac tại e vẽ hình luôn
a)cho AB=5cm,AC=7cm.tính BC
b) chung minh tam giac ABE=DBE
c) GỌI F là giao điểm của DEvà BA, chứng minh EF =EC
d) Chứng minh BE là trung trực của đoạn thẳng AD ai giúp tui với
\(\text{a)Xét }\Delta ABC\text{ vuông tại A có:}\)
\(BC^2=AB+AC^2\left(\text{định lí Py ta go}\right)\)
\(\Rightarrow BC^2=5^2+7^2=25+49=74\left(cm\right)\)
\(\Rightarrow BC=\sqrt{74}\left(cm\right)\)
\(\text{b)Xét }\Delta ABE\text{ và }\Delta DBE\text{ có:}\)
\(\widehat{BAE}=\widehat{BDE}=90^0\left(gt\right)\)
\(BE\text{ chung}\)
\(BA=BD\left(gt\right)\)
\(\Rightarrow\Delta ABE=\Delta DBE\left(c-g-c\right)\)
\(\text{c)Xét }\Delta AEF\text{ và }\Delta DEC\text{ có:}\)
\(\widehat{AEF}=\widehat{DEC}\left(\text{đối đỉnh}\right)\)
\(\widehat{FAE}=\widehat{CDE}=90^0\left(gt\right)\)
\(AE=DE\left(\Delta ABE=\Delta DBE\right)\)
\(\Rightarrow\Delta AEF=\Delta DEC\left(g-c-g\right)\)
\(\Rightarrow EF=EC\left(\text{hai cạnh tương ứng}\right)\)
\(\text{d)Gọi O là giao điểm của BE và AD}\)
\(\text{Xét }\Delta ABO\text{ và }\Delta DBO\text{ có:}\)
\(BO\text{ chung}\)
\(BA=BD\left(gt\right)\)
\(\widehat{ABO}=\widehat{DBO}\left(\Delta ABE=\Delta DBE\right)\)
\(\Rightarrow\Delta ABO=\Delta DBO\left(c-g-c\right)\)
\(\Rightarrow\widehat{AOB}=\widehat{DOB}\left(\text{hai góc tương ứng}\right)\)
\(\text{Mà chúng kề bù}\)
\(\Rightarrow\widehat{AOB}=\widehat{DOB}=\dfrac{180^0}{2}=90^0\)
\(\Rightarrow BE\perp AD\)
\(\text{Mà AO=DO}\left(\Delta AOB=\Delta DOB\right)\)
\(\Rightarrow BE\text{ là đường trung trực của đoạn thẳng AD}\)












