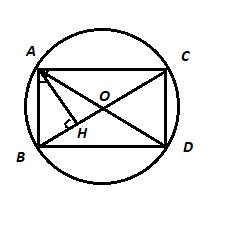
a, Do ΔABC vuông tại A, nội tiếp đường tròn (O) ⇒ BC là đường kính của đường tròn (O) (tính chất tam giác vuông nội tiếp đường tròn)
Xét tứ giác ABDC có:
Đường chéo AD và BC cắt nhau tại O mà O là trung điểm mỗi đường
⇒ Tứ giác ABDC là hình bình hành, lại có \(\widehat{BAC}=90^o\)
⇒ Tứ giác ABDC là hình chữ nhật (đpcm)
b, Do AH là đường cao ΔABC ⇒ \(\widehat{AHB}=90^o\)
Do ABDC là hình chữ nhật \(\Rightarrow\widehat{ACD}=90^o,\widehat{OAB}=\widehat{CDA}\) (CD//AB)
Xét ΔOAB có OA = OB = R ⇒ ΔOAB cân tại O \(\Rightarrow\widehat{OAB}=\widehat{OBA}hay\widehat{OAB}=\widehat{HBA}\)
⇒ \(\widehat{CDA}=\widehat{HBA}\)
Xét ΔACD và ΔAHB có:
\(\widehat{ACD}=\widehat{AHB}\left(=90^o\right)\)
\(\widehat{CDA}=\widehat{HBA}\)
⇒ ΔACD đồng dạng ΔAHB (g-g)
⇒ \(\dfrac{AC}{AD}=\dfrac{AH}{AB}\) (tỉ số đồng dạng)
\(\Rightarrow AB.AC=AH.AD\left(dpcm\right)\)
