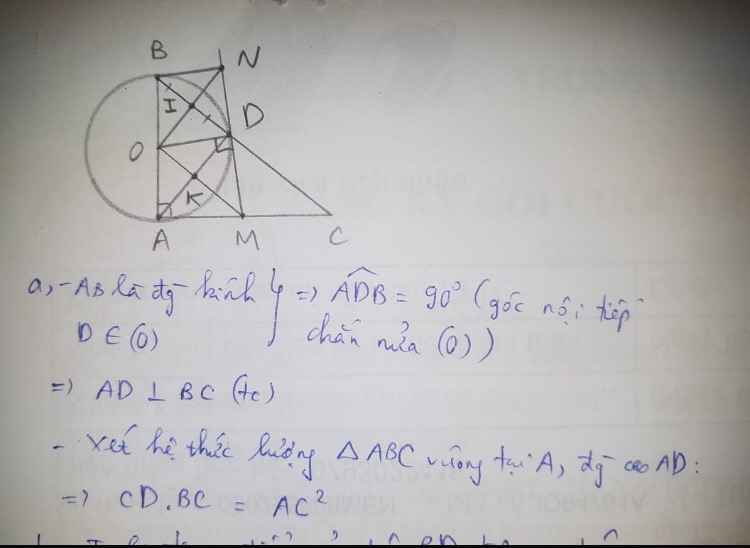Các câu hỏi tương tự
Cho tam giác ABC vuông tại A, ve đường tròn tâm O đường kính AC. Đường tròn (O) cắt BC tại điểm thứ hai I.Kẻ OM vuông góc với BC tại M, AM cắt (O) tại điểm thứ hai là Na) Chứng minh AM.MNCM2b) Từ I kẻ IH vuông góc với AC tại H. gọi K là trung điểm của IH. Tiếp tuyến tại I của (o) cắt AB tại P. Chứng minh 3 điểm C,K,P thẳng hàngc) Chứng minh OI là tiếp tuyến của đường tròn ngoại tiếp tam giác IMN.
Đọc tiếp
Cho tam giác ABC vuông tại A, ve đường tròn tâm O đường kính AC. Đường tròn (O) cắt BC tại điểm thứ hai I.Kẻ OM vuông góc với BC tại M, AM cắt (O) tại điểm thứ hai là N
a) Chứng minh AM.MN=CM2
b) Từ I kẻ IH vuông góc với AC tại H. gọi K là trung điểm của IH. Tiếp tuyến tại I của (o) cắt AB tại P. Chứng minh 3 điểm C,K,P thẳng hàng
c) Chứng minh OI là tiếp tuyến của đường tròn ngoại tiếp tam giác IMN.
1. cho tam giác ABC.Tia Ax nằm khác phía với AC đối với đường thẳng AB thỏa mãn góc xAB bằng góc ACB.chứng minh Ax là tiếp tuyến của đường tròn ngoại tiếp tam giác ABC2.cho nửa đường tròn (O) đường kính AB trên đoạn AB lấy điểm M,gọi H là trung điểm của AM.đường thẳng qua H vuông góc với AB cắt (O) tại C .đường tròn đường kính MB cắt BC tại I. CM HI là tiếp tuyến của đường tròn đường kính MB3.cho nửa đường tròn tâm O đường kính AB, C thuộc nửa đường tròn.vẽ CH vuông góc với AB(H thuộc AB),M là t...
Đọc tiếp
1. cho tam giác ABC.Tia Ax nằm khác phía với AC đối với đường thẳng AB thỏa mãn góc xAB bằng góc ACB.chứng minh Ax là tiếp tuyến của đường tròn ngoại tiếp tam giác ABC
2.cho nửa đường tròn (O) đường kính AB trên đoạn AB lấy điểm M,gọi H là trung điểm của AM.đường thẳng qua H vuông góc với AB cắt (O) tại C .đường tròn đường kính MB cắt BC tại I. CM HI là tiếp tuyến của đường tròn đường kính MB
3.cho nửa đường tròn tâm O đường kính AB, C thuộc nửa đường tròn.vẽ CH vuông góc với AB(H thuộc AB),M là trung điểm CH,BM cắt tiếp tuyến Ax của O tại P .chứng minh PC là tiếp tuyến của (O)
4.cho đường tròn O đường kính AB, M là một điểm trên OB.đường thẳng qua M vuông góc với AB tại M cắt O tại C và D. AC cắt BD tại P,AD cắt BC tại Q,AB cắt PQ tai I chứng minh IC,ID là tiếp tuyến của (O)
5.cho tam giác ABC nội tiếp đường tròn đường kính BC (AB<AC).T là một điểm thuộc OC.đường thẳng qua T vuông góc với BC cắt AC tại H và cắt tiếp tuyến tại A của O tại P.BH cắt (O) tại D. chứng minh PD là tiếp tuyến của O
6.cho tam giác ABC nội tiếp đường tròn O. phân giác góc BAC cắt BC tại D và cắt (O) tại M chứng minh BM là tiếp tuyến của đường tròn ngoại tiếp tam giác ABD
Bài 1: Điểm C nằm giữa hai điểm A và B. Vẽ đường tròn tâm O, đường kính AB và đường tròn tâm O đường kính BC. Vẽ tiếp tuyến chung của hai đường tròn tiếp xúc với đường tròn tâm O và tâm O tại D và E. AD cắt BE tại Ma) tam giác MAB là tam giác j?b) chứng minh CDME là hình chữ nhật và MC là tiếp tuyến của 2 đường tròn tâm O và tâm Oc) Kẻ tia Ex vuông góc với EA và tia By vuông góc với BA. Ex cắt By tại N. Chứng minh 3 điểm D,C.N thẳng hàng.Bài 2: Cho (O) và (O) cắt nhau tại A và B. Tiếp tuyến tại...
Đọc tiếp
Bài 1: Điểm C nằm giữa hai điểm A và B. Vẽ đường tròn tâm O, đường kính AB và đường tròn tâm O' đường kính BC. Vẽ tiếp tuyến chung của hai đường tròn tiếp xúc với đường tròn tâm O và tâm O' tại D và E. AD cắt BE tại M
a) tam giác MAB là tam giác j?
b) chứng minh CDME là hình chữ nhật và MC là tiếp tuyến của 2 đường tròn tâm O và tâm O'
c) Kẻ tia Ex vuông góc với EA và tia By vuông góc với BA. Ex cắt By tại N. Chứng minh 3 điểm D,C.N thẳng hàng.
Bài 2: Cho (O) và (O') cắt nhau tại A và B. Tiếp tuyến tại A của (O) cắt (O') tại D. Tiếp tuyến tại A của (O') cắt (O) tại C. Chứng minh rằng:
a) tam giác ABC đồng dạng với tam giác DBA
b) (AC/AD)^2 ( AC trên AD tất cả mũ 2) = BC/BD( AC trên AD tất cả mũ 2 bằng BC/BD)
c) Gọi E là điểm đối xứng của A qua B. Chứng minh ACED là tứ giác nội tiếp.
AB,AC là tiếp tuyến đường tròn tâm O, BD là đường kính đường tròn tâm O,AD cắt đường tròn tâm O tại E, AO cắt BC tại H.
a)Chứng minh AH.AO=AE.AD
b)Chứng minh HC là phân giác góc EHD
c)Gọi I là trung điểm ED.Tia OI cắt tiếp tuyến tại E của đường tròn tâm O tại S.Chứng minh S,B,C thằng hàng
Cho đường tròn (O), đường kính BC, A là điểm thuộc (O) sao cho ABAC, D là điểm nằm giữa O và C. Đường thẳng vuông góc với BC tại D cắt AC tại E và AB tại F.a/ Chứng minh các tứ giác ABDE và ADCF nội tiếpb/ Chứng minh góc AEF góc ABCc/ Tiếp tuyến tại A của đường tròn (O) cắt DE tại M. Chứng minh tam giác AME cân tại M.d/ Gọi I là tâm đường tròn ngoại tiếp tứ giác ADCF. Chứng minh OI vuông góc AC
Đọc tiếp
Cho đường tròn (O), đường kính BC, A là điểm thuộc (O) sao cho AB<AC, D là điểm nằm giữa O và C. Đường thẳng vuông góc với BC tại D cắt AC tại E và AB tại F.
a/ Chứng minh các tứ giác ABDE và ADCF nội tiếp
b/ Chứng minh góc AEF = góc ABC
c/ Tiếp tuyến tại A của đường tròn (O) cắt DE tại M. Chứng minh tam giác AME cân tại M.
d/ Gọi I là tâm đường tròn ngoại tiếp tứ giác ADCF. Chứng minh OI vuông góc AC
Cho đường tròn tâm O đường kính AB, lấy điểm C thuộc đường tròn tâm O, với điểm C không trùng A và B. Gọi I là trung điểm của dây AC, D là giao điểm của tia OI và tiếp tuyến của đường tròn tâm O tại A. a) Chứng minh tam giác ABC vuông. b) Chứng minh DC là tiếp tuyến của đường tròn tâm O. Chứng minh DC2DI.DO c) Tia phân giác của góc BAC cắt dây BC tại điểm E và cắt đường tròn tâm O tại F, với F không trùng với A. Chứng minh rằng FA.FEFB2
Đọc tiếp
Cho đường tròn tâm O đường kính AB, lấy điểm C thuộc đường tròn tâm O, với điểm C không trùng A và B. Gọi I là trung điểm của dây AC, D là giao điểm của tia OI và tiếp tuyến của đường tròn tâm O tại A. a) Chứng minh tam giác ABC vuông. b) Chứng minh DC là tiếp tuyến của đường tròn tâm O. Chứng minh DC2=DI.DO c) Tia phân giác của góc BAC cắt dây BC tại điểm E và cắt đường tròn tâm O tại F, với F không trùng với A. Chứng minh rằng FA.FE=FB2
Làm giúp mình 2 bài này với, mai mình phải nộp rồi!!!Bài 1: Từ điểm A nằm ngoài đường tròn (O;R), vẽ 2 tiếp tuyến AB, AC với đường tròn.a) Chứng minh tứ giác OBAC nội tiếp và OA vuông góc BC tại Hb) Vẽ đường kính CD của đường tròn (O;R), AD cắt (O) tại M. Chứng minh: góc BHM góc MACc) Tia BM cắt AO tại N. Chứng minh NANHd) Vẽ ME là đường kính đường tròn (O), gọi I là trung điểm DM. Chứng minh: 3 điểm B, I, E thẳng hàng và BI song song MH.Bài 2: Cho tam giác ABC vuông tại A. Vẽ đường tròn tâm O...
Đọc tiếp
Làm giúp mình 2 bài này với, mai mình phải nộp rồi!!!
Bài 1:
Từ điểm A nằm ngoài đường tròn (O;R), vẽ 2 tiếp tuyến AB, AC với đường tròn.
a) Chứng minh tứ giác OBAC nội tiếp và OA vuông góc BC tại H
b) Vẽ đường kính CD của đường tròn (O;R), AD cắt (O) tại M. Chứng minh: góc BHM = góc MAC
c) Tia BM cắt AO tại N. Chứng minh NA=NH
d) Vẽ ME là đường kính đường tròn (O), gọi I là trung điểm DM. Chứng minh: 3 điểm B, I, E thẳng hàng và BI song song MH.
Bài 2:
Cho tam giác ABC vuông tại A. Vẽ đường tròn tâm O đường kính AC cắt BC tại H. Gọi I là trung điểm của HC. Tia OI cắt (O) tại F
a) Chứng minh AH là đường cao của tam giác ABC và AB^2= BH. BC
b) Chứng minh: Tứ giác ABIO nội tiếp
c) Chứng minh: AF là tia phân giác của góc HAC
d) AF cắt BC tại D. Chứng minh: BA=BD
Cho tam giác ABC nội tiếp nửa đường tròn đường kính BC (AB < AC) . Gọi K là trung điểm của AC
a) Chúng minh : OK vuông góc AC
b) Tiếp tuyến tại C của (O) cắt tia OK tại D . Gọi T là giao điểm của BD và (O) . Chứng minh : DK.DO = DT.DB
c) Vẽ AH vuông góc với BC tại H . Gọi I là giao điểm của AH và BD . Tia CI cắt đường thẳng AD tại E . Chứng minh : EB là tiếp tuyến của (O)
Từ điểm A ở ngoài đường tròn (O;R) vẽ 2 tiếp tuyến AB và AC (B, C là tiếp điểm). Gọi H là giao điểm của AO và BC.
a) Chứng minh AO là đường trung trực của BC
b) Vẽ đường kính CD của (O), AD cắt (O) tại E. Chứng minh AB^2 = AE.AD
c) Tiếp tuyến tại E của (O) cắt AB và AC lần lượt tại M và N. Chứng minh chu vi tam giác AMN = 2AB
d) MN cắt AO tại I, EO cắt BC tại P. Chứng minh AE // IP