Question

Cho tam giác ABC vuông tại A; đường phân giác BE. Kẻ EH vuông góc với BC (H thuộc BC). Gọi K là giao điểm của AB và HE. Chứng minh rằng:

a) tam giác ABE= tam giác HBE.

b) BE là đường trung trực của đoạn thẳng AH.

c) EK= EC.

d) AE< EC.

Answer 1

a, xét 2 tam giác vuông ABE và HBE có:

          BE cạnh chung

         \(\widehat{ABE}\)=\(\widehat{HBE}\)(gt)

=> tam giác ABE =tam giác HBE(CH-GN)

b) gọi O là giao điểm của BE và AH

xét tam giác OAB và tam giác OHB có:

          OB chung

         \(\widehat{OBA}\)=\(\widehat{OBH}\)(gt)

         AB=HB(theo câu a)

=> tam giác OAB=tam giác OHB(c.g.c)

=> OA=OH=> O là trung điểm của AH(1)

\(\widehat{AOB=\widehat{HOB}}\)mà 2 góc này ở vị trí kề bù nên \(\widehat{AOB=\widehat{HOB}}\)=90 độ => BO\(\perp\)AH(2)

từ (1) và (2) => BE là trung trực của AH

c)xét 2 tam giác vuông EAK và HEC có:

       AE=EH

      \(\widehat{AEK=\widehat{HEC}}\)(đối đỉnh)

=> tam giác EAK=tam giác HEC(cạnh góc vuông-góc nhọn)

=> EK=EC

d) trong tam giác vuông AEK có: AE<EK(vì cạnh huyền>cạnh góc vuông) mà EK=EC=> AE<EC

Answer 2

--thanks you very much--

Answer 3

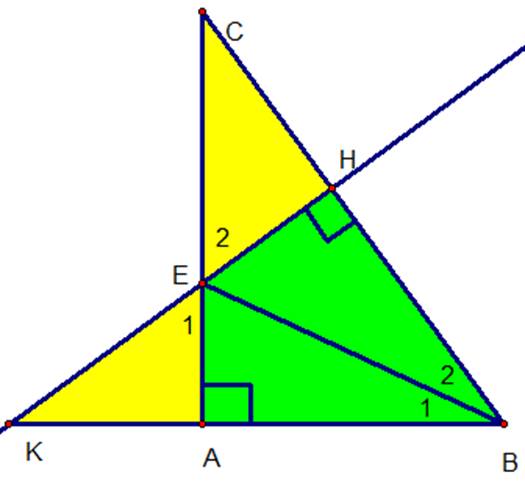
Xét ΔABE và ΔHBE, ta có:

 (gt)

( BE là đường phân giác BE).

BE là cạnh chung.

=> ΔABE = ΔHBE

2. BE là đường trung trực của AH :

BA =BH và EA = EH (ΔABE = ΔHBE)

=> BE là đường trung trực của AH .

3. EK = EC

Xét ΔKAE và ΔCHE, ta có :

 (gt)

EA = EH (cmt)

( đối đỉnh).

=> ΔKAE và ΔCHE

=> EK = EC

4. EC > AC

Xét ΔKAE vuông tại A, ta có :

KE > AE (KE là cạnh huyền)

Mà : EK = EC (cmt)

=> EC > AC.

cre baji