Question

Cho tam giác ABC vuông tại A, đường phân giác AD. Gọi M, N là chân đường vuông góc kẻ từ D đến AB, AC. Chứng minh rằng tứ giác AMDN là hình vuông.

Answer 1

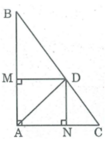
Xét tứ giác AMDN, ta có: ∠ (MAN) = 90 0 (gt)

DM ⊥ AB (gt)

⇒ ∠ (AMD) =  90 0

DN ⊥ AC (gt) ⇒ ∠ (AND) =  90 0

Suy ra tứ giác AMDN là hình chữ nhật

(vì có ba góc vuông), có đường chéo AD là đường phân giác của A

Vậy hình chữ nhật AMDN là hình vuông

Answer 2

                 Vì M, N là chân đường vuông góc kẻ từ D đến AB, AC =>tứ giác AMDN là hình chữ nhật (có 3 góc vuông).

*Xét AMDN, có: (gt) =>AMDN là hình chữ nhật.

Ta lại có: AD là đường phân giác (gt) =>AMDN là hình vuông(đpcm).

CHÚC BẠN HỌC TỐT NHA!!